त्रिभुज कैलकुलेटर

निम्नलिखित सूत्र समीकरणों में सही हैं:
साइन नियम:
a / b = साइन अल्फा / साइन बीटा
कोसाइन नियम:
a ^ 2 = b ^ 2 + c ^ 2-2bc cos अल्फ़ा

त्रिभुज

त्रिकोण क्या है?

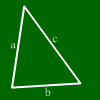
यहां हम एक त्रिभुज देख सकते हैं।
एक त्रिभुज के तीन पक्ष और तीन कोने होते हैं।
प्रत्येक कोने में, एक आंतरिक कोण होता है, अर्थात उस कोने पर समाप्त होने वाले पक्षों के बीच का कोण।
एक त्रिभुज के सभी आंतरिक कोणों का योग हमेशा 180 डिग्री होता है।

त्रिभुज किस सूचना द्वारा विशिष्ट रूप से निर्धारित किया जाता है?

एक त्रिभुज हमेशा अपनी तीन भुजाओं की लंबाई से निर्धारित होता है। यह दो कोणों और एक पक्ष द्वारा निर्धारित किया जाता है, दो पक्षों द्वारा ताल और उन पक्षों के बीच का कोण।
एक त्रिकोण को तीन अन्य मूल्यों द्वारा भी निर्धारित किया जा सकता है। लेकिन उदाहरण के लिए, यदि आपको दो तरफ और ऊंचाई एक तरफ मिली, तो उन लंबाई के साथ एक से अधिक संभावित त्रिकोण हैं।

त्रिभुज की ऊँचाई कितनी है?

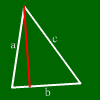
ऊंचाई एक तरफ और विरोधी कोने के बीच की दूरी है।

एक त्रिकोण में क्या गणना की जा सकती है?

क्षेत्र की गणना किसी भी पक्ष और संबंधित ऊंचाई के लिए (पक्ष * ऊंचाई) / 2 के रूप में की जा सकती है।
पक्षों और कोणों की गणना साइन और कोसाइन का उपयोग करके की जा सकती है। निम्नलिखित सूत्र पकड़:
a / साइन (अल्फा) = b / साइन (बीटा) (साइन नियम)
इसके अलावा, तीन पक्षों के लिए, बी, सी और कोण अल्फा एक का विरोध:
a ^ 2 = b ^ 2 + c ^ 2-2bc cos अल्फ़ा (cosine rule)

त्रिकोण पर क्या दिलचस्प रेखाएं मौजूद हैं?

दिलचस्प रेखाएं लंबवत द्विभाजक, कोण द्विभाजक, मध्य रेखाएं हैं और ऊंचाइयों।

क्या विशेष मामले दिलचस्प हैं?

दिलचस्प विशेष मामले समद्विबाहु त्रिकोण हैं, समबाहु त्रिभुज और समकोण त्रिभुज।

अधिक जानकारी के लिए, माउस को नीचे दिए गए शब्दों से ऊपर ले जाएँ और संबंधित रेखा को त्रिभुज पर चिह्नित किया जाएगा।


पक्ष a पक्ष b पक्ष c
अल्फा कोण कोण बीटा कोण गामा
ऊंचाई पर a ऊंचाई पर b ऊंचाई पर c
माध्य रेखा a माध्य रेखा b माध्य रेखा c
अल्फा के कोण द्विभाजक बीटा के कोण द्विभाजक गामा के कोण द्विभाजक
क्षेत्र