Aquí puedes calcular la altura de un triángulo, los ángulos de un triángulo, los lados de un triángulo
y el área de un triángulo. Se aplica las siguientes fórmulas a un triángulo:
Teorema de los senos:
a / b = sen alpha / sen beta
Teorema del coseno:
a^2=b^2+c^2-2bc cos alpha
Triángulos
¿Qué es un triángulo?
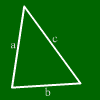
Aquí vemos un triángulo.
Un triángulo tiene tres lados y tres ángulos.
En cada ángulo, se encuentra un ángulo interior, es decir, el ángulo entre dos lados acabando en este mismo ángulo.
La suma de los ángulos interiores es siempre 180 grados.
¿Qué características determinan un triángulo?
Un triángulo siempre esta determinado por la longitud de sus tres lados. También esta determinado por dos ángulos y un lado o por dos lados y el ángulo entre ambos lados.
Un triángulo se puede también determinar por otros tres valores. Pero por ejemplo, si dos lados y la altura en un lado estan conocidas hay varios triángulos posibles que tengan estas medidas.
¿Qué es la altura de un triángulo?
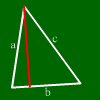
La altura es la distancia entre un lado y su ángulo opuesto.
¿Qué tipo de calculaciones se puede realizar en un triángulo?
El área se obtiene calculando (lado*altura)/2 para cualquier lado y su altura correspondiente.
Los lados y ángulos se obtiene usando el seno y coseno. Se aplica las siguientes fórmulas:
a/sen(alpha)=b/sen(beta) (teorema de los senos)
También se aplica para tres lados a,b,c y ángulo alpha opuesto a a:
a^2=b^2+c^2-2bc cos alpha (teorema del coseno)
¿Qué líneas interesantes contienen triángulos?
Líneas interesantes son las mediatrices y bisectrices de un ángulo, las medianas
y las alturas.
¿Qué casos especiales de triángulos pueden ser interesantes?
Casos interessantes son el triángulo isósceles, el
triángulo equilátero y el triángulo rectángulo.
Para más información mueve el mouse sobre las palabras abajo y la línea correspondiente estará marcada en el dibujo del triángulo.
Lado a,
Lado b,
Lado c
Ángulo alpha,
Ángulo beta,
Ángulo gamma
Altura correspondiente a la base a,
Altura correspondiente a la base b,
Altura correspondiente a la base c
mediana correspondiente al lado a,
mediana correspondiente al lado b,
mediana correspondiente al lado c
bisectriz del ángulo alpha,
bisectriz del ángulo beta,
bisectriz del ángulo gamma
área