La ley de los signos



Introduce tu función aquí
Consejos: Introduce como 3*x^2
como 3/5 y
como (x+1)/(x-2x^4)


¿Qué es la ley de los signos?

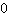
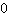
Para encontrar extremos relativos se usa la ley de los signos(cambio de signos). Así podemos diferenciar si una función cuya derivada es 0 tiene un punto máximo o mínimo o un punto de silla. Aquí tienes tres ejemplos en los que la función tiene la pendiente 0 en (1|2):

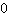
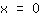
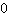
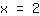
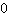
Esta función tiene la pendiente 0 en (1|2) y un punto máximo. En x=0 la gráfica asciende, es decir, la derivada es más grande que 0. En x=2 la gráfica desciende, es decir, la derivada es inferior a 0. Esto significa que alrededor de un punto máximo el signo de la derivada es + delante del punto de inflexión y - detrás del punto de inflexión. Esto quiere decir que la derivada cambia los signos de + a - .



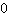
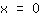
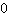
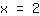
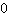
Esta función tiene la pendiente 0 en (1|2) pero un punto mínimo. En x=0 la gráfica desciende, es decir, la derivada es inferior a 0. En x=2 la gráfica asciende, es decir, la derivada es mayor que 0. Esto implica que en un mínimo. El signo de la derivada es - delante del punto de inflexión y + después del punto de inflexión. Esto significa que la derivada cambia los signos de - a +.



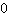
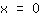
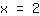
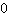
Esta función tiene la pendiente 0 en (1|2) pero no tiene punto de inflexión. Se puede ver que la gráfica asciende en x=0 así como en x=2. Esto implica que no hay punto de inflexión si la derivada no cambia signos. Un punto así (que no es punto de inflexión pero tiene la derivada 0) se llama punto de silla o punto de ensilladura.

¿Cómo se usa la ley de los signos?

  • Primero tienes que derivar tu función.
  • Después calcula las raíces de la derivada. Sólo las raíces pueden ser coordenadas de X de puntos extremos.
  • Por último inserta valores de x que se encuentran cerca de las raíces de la derivada en la derivada. Si la derivada cambia signos encontraste un punto extremo. En caso contrario, no hay puntos extremos.

    • ¿Por qué la ley de los signos es un criterio suficiente?

    Es necesario que la derivada es 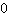0 para obtener un punto extremo (es decir, es siempre el caso en un punto extremo). Pero no es suficiente. Sólo porque la derivada es 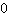0 no es dicho que no hay un punto extremo (véase arriba sobre el punto de silla).
    Si la derivada aparte de ser 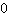0, también cambia los signos entonces sí que tenemos un punto extremo. En matemáticas decimos que la derivada 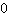0 y el cambio de los signos es suficiente para poder decir que tenemos un punto extremo.

    ¿Puedo ver un ejemplo?

    Por supuesto. Esto es Mathepower. Introduce tu función arriba y Mathepower calcula los puntos de inflexión paso a paso.