Qual a finalidade da troca de sinais?
Ao verificar a mudança de sinal, você pode verficar se um função com derivada
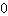
tem um ponto extremo mínimo / máximo ou um ponto de sela. Veja três exemplos onde a função tem inclinação
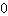
em (1|2):
Esta função tem inclinação
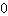
em (1|2) e um ponto extemo máximo. Em
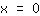
o gráfico sobe, ou seja, aqui a derivada é maior que
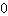
. Em
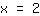
o gráfico desce, ou seja, a derivada menor que
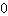
. Isso significa que no ponto extremo máximo, o sinal da derivada é + antes e - depois do ponto extremo. Ou seja, a derivada muda o sinal de + para -.
Esta função tem inclinação
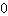
em (1|2) mas um ponto extemo mínimo. Em
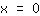
o gráfico desce, ou seja, aqui a derivada é menor que
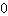
. Em
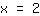
o gráfico sobe, ou seja, a derivada é maior que
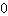
. Isso implica que no ponto extremo mínimo, o sinal da drivada é - antes e + depois do ponto extremo. Significa que os sinais da derivada mudaram de - para +.
Esta função também tem inclinação
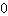
em (1|2), mas não tem um ponto extremo. Perceba que o gráfico ascende em
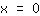
como também em
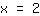
. Significa que você não tem um ponto extremo se a derivada não mudar o sinal. Tal ponto (que não é um extremo mas tem a derivada
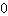
é chamado de ponto de sela.
Qual critério usar para a troca de sinais?
- Primeiro encontre a derivada da sua função.
- Então calcule a raíz da derivada. Somente essas raízes podem ser as coordenadas-x dos pontos extremos.
- Então insira os valores-x próximo as raízes da derivada na derivada. Caso a derivada mude o sinal em torno da derivada, você encontrou um ponto extremo. Caso contrário, não.
Por que a mudança de sinais é um critério suficiente?
A derivada ser 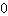é necessário para um ponto extremo. Mas não é porque a derivada é 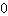que obrigatoriamente terá um ponto extremo (confira sobre pontos de sela acima).
Se a derivada é 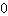e também muda os sinais, então você deve ter um ponto extremo. Na matmática, dizemos que derivada sendo 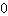e muda o sinal é suficiente para ter um ponto extremo.
Posso ver mais exemplos?
Claro. Insira sua função qie a Mathepower calculará seus pontos extremos passo a passo.