O que é uma função linear?
Função linear é uma função cujo gráfico é uma linha. Exemplo:
Seu exercício: 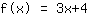
Aqui está o gráfico da sua função.
|
|
- Raízes á -1.333
- intercepção do eixo-y á (0|4)
|
O gráfico de uma função linear sempre será uma linha.
Função linear pode também ser chamada de correlação linear.
O que é a inclinação de uma função?
A inclinação da função é representada pelo número em frente ao x. Mostra como unidades devem se mover (se pra cima ou pra baixo). Caso você mova para a direita. Exemplo:
Seu exercício: 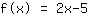
Aqui está o gráfico da sua função.
|
|
- Raízes á 2.5
- intercepção do eixo-y á (0|-5)
|
Vemos que essa função tem inclinação
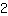
. Se movermos um quadrado a direita de qualquer ponto no gráfico, temos que mover dois quadrados acima para ficar no gráfico novamente.
Outro exemplo: Dessa vez com inclinação negativa:
Seu exercício: 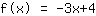
Aqui está o gráfico da sua função.
|
|
- Raízes á 1.333
- intercepção do eixo-y á (0|4)
|
Esta função tem inclinação
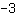
. Significa que sempre que movermos um quadrado a direita, temos que mover
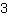
para baixo.
O que é a linha intercepto-y de uma função linear?
A linha intercepto-y é o número no final da função. Como o nome diz, mostra onde a linha cruza o eixo-y. Se olhar o gráfico, você verá que
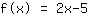
o eixo-y cruza em
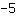
e
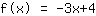
o eixo-y cruza em
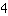
Como calcular a equação da linha a partir de um ponto e da inclinação?
Você deve inserir o ponto na equação, ou seja, uma coordenada para x e outra para f(x). Exemplo: Sabemos que nossa função tem inclinação
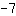
e passa por (-2|5).
Seu exercício:
Ponto (-2|5); Inclinação -7;
Seu exercício: 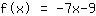
Aqui está o gráfico da sua função.
|
|
- Raízes á -1.286
- intercepção do eixo-y á (0|-9)
Isto é o que a Mathepower calculou:
Calcule a interceptação do eixo-y b inserindo:
Forma geral da função linear: f(x)=mx+b
Insira 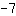 para m, para m, 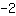 para x e para x e 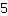 para f(X) para f(X)
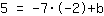 | | | Multiplique 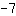 por por 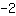 |
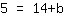 | | | Troque os dois lados da equação. |
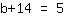 | | | 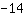 |
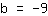 | | |
Então, a intercepção do eixo-y está em 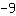
Portanto, temos a equação da função 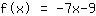
|
Como calculo a equação de uma função a partir de dois pontos?
Primeiro, temos que calcular a inclinação m inserindo as coordenadas x e y dos dois pontos. Na fórmula
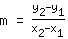
. Significa que: Você calcula a distância das coordenadas y e divide pela distância das coordenadas x. Exemplo:
Seu exercício:
Ponto (1|2); Ponto (3|8);
Seu exercício: 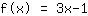
Aqui está o gráfico da sua função.
|
|
- Raízes á 0.333
- intercepção do eixo-y á (0|-1)
Isto é o que a Mathepower calculou:
Para calcular a inclinação m, use a fórmula 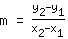 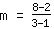 | | | Adicione  a a 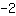 |
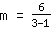 | | | Adicione 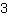 a a 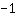 |
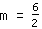 | | | Divida 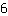 por por 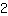 |
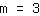 | | |
Calcule a interceptação do eixo-y b inserindo:
Forma geral da função linear: f(x)=mx+b
Insira 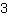 para m, para m, 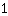 para x e para x e 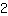 para f(X) para f(X)
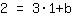 | | |
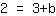 | | | Troque os dois lados da equação. |
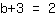 | | | 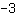 |
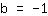 | | |
Então, a intercepção do eixo-y está em 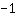
Portanto, temos a equação da função 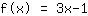
|
Como vemos ,a inclinação foi calculada primeiro. Para achar a equação da função, você deve inserir um ponto e obter uma equação que te informe a interseção do eixo-y.
Posso ver mais exemplos?
Claro. Insira seus próprios exemplos acima e eles serão calculados passo a passo. (Essa é a idéia da Mathepower:
Você não só vê exemplos prontos, mas também explicações dos seus próprios cálculos!)