Qu'est-ce qu'une fonction linéaire?
Une fonction linéaire est une fonction dont le graphique est une droite. Voici un exemple:
Votre exercice: 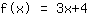
Ceci est le graphique de votre fonction.
|
|
- Racines à -1.333
- Ordonnée à l'origine à (0|4)
|
Le graphique d'une fonction linéaire est toujours une droite.
Dans l'algèbre linéaire on utilise plus souvent corrélation linéaire plutôt que fonction linéaire.
Qu'est que la pente d'une fonction linéaire?
La pente d'une fonction linéaire correspond au coefficient de la variable x. Il indique de combien les ordonnées (axe y) doivent monter ou descendre si vous vous déplacez d'une unité sur l'axe x. Exemple:
Votre exercice: 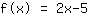
Ceci est le graphique de votre fonction.
|
|
- Racines à 2.5
- Ordonnée à l'origine à (0|-5)
|
Nous voyons que cette fonction a une pente
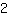
. Si nous allons une unité à droite de n'importe quel point du graphique, l'ordonnée de la fonction monte de deux unités.
Un autre exemple, cette fois avec une pente négative:
Votre exercice: 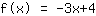
Ceci est le graphique de votre fonction.
|
|
- Racines à 1.333
- Ordonnée à l'origine à (0|4)
|
Cette fonction linéaire a une pente de
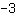
. Cela signifie que chaque fois que nous allons d'une unité vers la droite, nous devons descendre de trois unités pour être à nouveau sur le graphique.
Quelle est l'ordonnée à l'origine d'une fonction linéaire?
L'ordonnée à l'origine est le terme constate de la fonction. C'est-à-dire quand la x est égal à
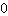
, ou aussi quand la fonction coupe l'axe des y. Si vous jetez un œil sur les graphiques de deux fonctions ci-dessus, vous voyez que
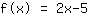
coupe l'axe y à
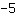
et
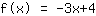
coupe l'axe y à
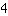
.
Comment calculer l'équation de la fonction linéaire à partir d'un point et de sa pente?
Vous devez insérer le point dans l'équation de la droite, c'est-à-dire la coordonnée dans x et f (x). Voici un exemple: supposons que notre fonction a une pente
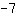
et passe par
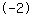
|
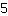
.
Votre exercice:
Point (-2|5); Pente -7;
Votre exercice: 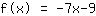
Ceci est le graphique de votre fonction.
|
|
- Racines à -1.286
- Ordonnée à l'origine à (0|-9)
Voici ce que Mathepower a calculé:
Calcul de l'ordonnée à l'origine p en insérant:
Forme générale de la fonction linéaire: f(x)=mx+b
Insérez 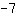 dans m, dans m, 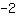 dans x et dans x et 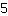 dans f(x). dans f(x).
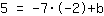 | | | Multiplier 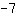 par par 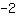 |
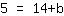 | | | Échangez les deux membres de l'équation. |
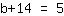 | | | 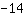 |
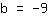 | | |
Ainsi, l'ordonnée à l'origine est 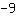
Par conséquent, l'équation de la fonction est 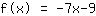
|
Comment calculer l'équation d'une fonction linéaire à partir de deux points donnés?
Tout d'abord, nous devons calculer la pente m en insérant les coordonnées x et y des points dans la formule m =
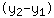
/
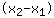
. Ça signifie: Vous calculez la différence des coordonnées y et la divisez par la différence des coordonnées x. Voici un exemple:
Votre exercice:
Point (1|2); Point (3|8);
Votre exercice: 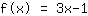
Ceci est le graphique de votre fonction.
|
|
- Racines à 0.333
- Ordonnée à l'origine à (0|-1)
Voici ce que Mathepower a calculé:
Calcule de la pente m: utilisez la formule 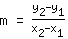 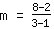 | | | ajouter  et et 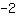 |
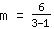 | | | ajouter 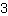 et et 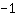 |
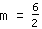 | | | Diviser 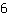 par par 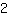 |
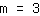 | | |
Calcul de l'ordonnée à l'origine p en insérant:
Forme générale de la fonction linéaire: f(x)=mx+b
Insérez 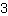 dans m, dans m, 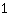 dans x et dans x et 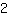 dans f(x). dans f(x).
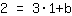 | | |
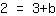 | | | Échangez les deux membres de l'équation. |
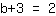 | | | 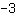 |
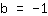 | | |
Ainsi, l'ordonnée à l'origine est 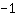
Par conséquent, l'équation de la fonction est 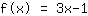
|
Comme nous pouvons le voir, la pente a été calculée en premier. Pour trouver l'équation de la fonction, vous devez insérer un point et obtenir une équation qui donne l'intersection à l'ordonnée y, le terme constant q.
Puis-je voir plus d'exemples?
Bien sûr. Entrez simplement vos données ci-dessus et vos fonctions seront calculées immédiatement étape par étape. C'est l'idée de Mathepower:
vous ne regardez pas seulement quelques explications déjà faites, mais vous obtenez vos propres calculs expliqués!