Wat is een lineaire functie?
Een lineaire functie is een functie waarvan de grafiek een lijn is. Hier is een voorbeeld:
Jouw oefening: 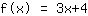
Dit is de grafiek van uw functie.
|
|
- Nulpunten bij -1.333
- y-as snijpunt bij (0|4)
|
De grafiek van een lineaire functie is altijd een lijn.
Een soortgelijk woord als lineaire functie is lineaire correlatie.
Wat is de helling van een lineaire functie?
De helling van een lineaire functie komt overeen met het getal voor de x. Het vertelt hoe veel eenheden je omhoog / omlaag moet gaan als je een eenheid naar rechts gaat. Voorbeeld:
Jouw oefening: 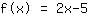
Dit is de grafiek van uw functie.
|
|
- Nulpunten bij 2.5
- y-as snijpunt bij (0|-5)
|
We zien dat deze functie helling
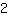
heeft. Als we een hokje naar rechts van een willekeurig punt in de grafiek gaan, moeten we twee vierkanten omhoog om weer op de grafiek te komen.
Een ander voorbeeld, dit keer met negatieve helling:
Jouw oefening: 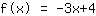
Dit is de grafiek van uw functie.
|
|
- Nulpunten bij 1.333
- y-as snijpunt bij (0|4)
|
Deze lineaire functie heeft helling
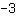
. Dit betekent dat wanneer we een hokje naar rechts gaan, we drie hokjes naar beneden moeten gaan om weerop de grafiek te komen.
Wat is het snijpunt met de y-as van een lineaire functie?
Het snijpunt met de y-as is het getal aan het einde van de functie. Zoals de naam al zegt, geeft het aan waar de functie de y-as snijdt. Als jij kijkt eens naar de functiegrafieken, zie je dat
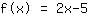
de y-as snijdt bij
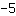
en
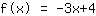
de y-as snijdt bij
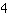
.
Hoe bereken je de vergelijking van de lijn m.b.v. een punt en de helling?
Je moet het punt in de vergelijking invoegen, d.w.z. de ene coordinaat voor x en de andere voor f(x). Hier is een voorbeeld: laten we aannemen dat we weten dat onze functie helling
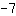
heeft en door het punt (-2|5) loopt.
Jouw oefening:
punt (-2|5); helling -7;
Jouw oefening: 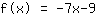
Dit is de grafiek van uw functie.
|
|
- Nulpunten bij -1.286
- y-as snijpunt bij (0|-9)
Dit is wat Mathepower heeft berekend:
Bereken b (van het y-as snijpunt (0|b)) door in te voegen:
Algemene vorm van de lineaire functie: f(x)=mx+b
Invoeren 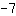 voor m, voor m, 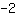 voor x en voor x en 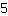 voor f(x) voor f(x)
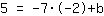 | | | Vermenigvuldig 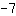 met met 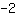 |
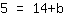 | | | Verwissel beide kanten van de vergelijking |
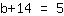 | | | 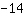 |
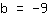 | | |
Het snijpunt van de y-as is dus bij 
Daarom is de vergelijking van de functie 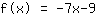
|
Hoe bereken je de vergelijking van een lineaire functie uit twee gegeven punten?
Eerst moeten we de helling m berekenen door de x- en y- coordinaten van de punten in te voegen in de formule m =
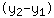
/
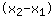
. Dit houdt in: Je berekent het verschil van de y-coordinaten en deelt het door het verschil van de x-coordinaten. Hier is een voorbeeld:
Jouw oefening:
punt (1|2); punt (3|8);
Jouw oefening: 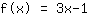
Dit is de grafiek van uw functie.
|
|
- Nulpunten bij 0.333
- y-as snijpunt bij (0|-1)
Dit is wat Mathepower heeft berekend:
Om de helling m te berekenen, gebruik de formule 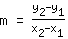 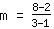 | | | optellen van  en en 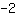 |
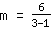 | | | optellen van 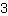 en en 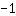 |
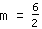 | | | Deel 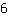 door door 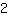 |
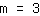 | | |
Bereken b (van het y-as snijpunt (0|b)) door in te voegen:
Algemene vorm van de lineaire functie: f(x)=mx+b
Invoeren 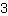 voor m, voor m, 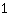 voor x en voor x en 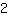 voor f(x) voor f(x)
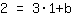 | | |
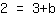 | | | Verwissel beide kanten van de vergelijking |
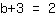 | | | 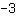 |
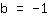 | | |
Het snijpunt van de y-as is dus bij 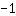
Daarom is de vergelijking van de functie 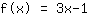
|
Zoals we kunnen zien, werd de helling eerst berekend. Om de vergelijking van de functie te vinden, moet je een punt invoegen en je vindt een vergelijking die het snijpunt van de y-as geeft.
Kan ik meer voorbeelden zien?
Natuurlijk. Voer hierboven gewoon je eigen voorbeelden in en ze worden direct stap voor stap berekend. (Dit is het idee van Mathepower:
Je kijkt niet alleen naar voorgekookte verklaringen, maar je krijgt je eigen berekeningen uitgelegd!)