Differentieren

Wat is de afgeleide?

De afgeleide van een functie op punt x geeft de helling aan van de grafiek van de functie op punt x, dat wil zeggen, welke helling de raaklijn in het punt (x|f(x)) heeft.

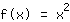
Voorbeeld: de normaalparabool f_f(x)=x^2

heeft de raaklijn 2x-1

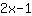
in (1|1), d.w.z. helling

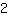
. De afgeleide van de normaalparabool bij x =

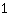
is dus gelijk aan

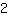
Wat is het verschil tussen de afgeleide en de afgeleide functie?

De afgeleide functie f '(x) van f (x) is een functie die de afgeleide (waarde) geeft voor elke gegeven x. Dit betekent: Om erachter te komen wat de helling van f bij x is, hoef je alleen maar x in de afgeleide functie in te voeren . De afgeleide functie wordt ook vaak kortweg de afgeleide genoemd.

En hoe bereken je een afgeleide?

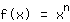
Voordat de differentieerregels werden ontdekt, moest men het differentiequotient voor elk punt afzonderlijk berekenen. Door differentieerregels te gebruiken, wordt het eenvoudiger: eerst bereken je de afgeleide van machtsfuncties. f_f(x)=x^n

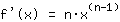
. Dit is simpel f_f'(x)=nx^(n-1)

. Volgende regels maken het mogelijk de afgeleide te berekenen van een willekeurige polynoom functie, welke slechts de som is van producten van machtsfuncties met getallen. Dus je hebt slechts volgende regels nodig:

de constante factor regel:
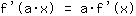
en de somregel: de afgeleide van de functie 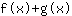is gelijk aan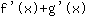

Voor meer ingewikkelde functies zijn er verdere differentieerregels nodig:

de productregel: de afgeleide van functie 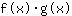is gelijk aan
de quotientregel: de afgeleide van functie 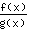is gelijk aan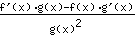
de kettingregel: de afgeleide van functie 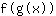is gelijk aan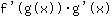

Waarom bepaal je de nulpunten van een afgeleide?

De nulpunten van de afgeleide zijn belangrijke punten van de grafiek. Bij extreme waarden (maximum of minimum) is de eerste afgeleide gelijk aan nul. (Let op: het omgekeerde geldt niet - alleen omdat de eerste afgeleide nul is, hoeft een punt geen extreme waarde te zijn! Bekijk het tekenwissel criterium voor meer informatie.) Bij een buigpunt is de tweede afgeleide nul. Dus je ervaart veel over een functie door de afgeleide gelijk te stellen aan nul en de vergelijking op te lossen.