Derivate

Derivation Derivate Dérivée de fonction الإشتقاق वà¥à¤¯à¥à¤¤à¥à¤ªà¤¤à¥à¤¤à¤¿ 导数 Differentieren Derivación derivação



Inserisci qui la funzione da derivare.
Suggerimenti: inserisci come 3*x^2 ,
come 3/5 e
come (x+1)/(x-2x^4)



Che cosa è una derivata?

La derivata di una funzione in un punto x indica la pendenza del grafico della funzione in quel punto, cioè che pendenza ha la retta tangente al grafico nel punto (x|f(x)).

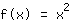
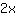
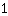
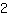
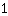
Esempio: la parabola f_f(x)=x^2 ha nel punto (1|1) la tangente 2x - 1, cioè pendenza 2. La derivata della parabola nel punto x = 1 è, infatti, uguale a 2.

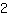
Qual è la differenza tra la derivata e la funzione derivata?

La funzione derivata f'(x) di una funzione f(x) è una funzione che indica la pendenza per ogni valore di x. Ciò significa che, per calcolare la pendenza di f nel punto x, basta sostituire x nella funzione derivata . Nella pratica si utilizza spesso solo il termine derivata anziché quello di funzione derivata.

E come si calcola una derivata?

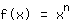
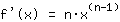
Prima di iniziare a usare le regole di derivazione, per trovare la derivata della funzione bisogna calcolare il rapporto incrementale singolarmente per ogni punto . Con le regole di derivazione le cose si semplificano: iniziamo con la derivata di funzioni di potenza f_f(x)=x^n. Essa è semplicemente f_f'(x)=nx^(n-1). Con altre regole si riesce a calcolare la derivata di una qualsiasi funzione polinomiale, data dalla somma di prodotti di funzioni di potenza e numeri . Dobbiamo solo conoscere due regole:
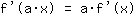
  • la regola della costante: f_f'(a*x)=a*f_f'(x)
  • la regola della somma: la derivata della funzione 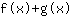è uguale a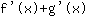
Per funzioni più complesse servono altre regole come:
  • la regola del prodotto: la derivata della funzione 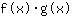è uguale a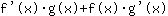
  • la regola del quoziente: la derivata della funzione 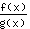è uguale a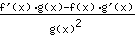
  • la regola della catena: la derivata della funzione 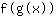è uguale a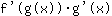

A che serve trovare gli zeri di una funzione?

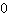
Gli zeri, o radici reali, di una funzione sono tra i più importanti punti del grafico. Nei punti di massimo o di minimo, detti punti estremanti di una funzione, la derivata è nulla (attenzione perché il viceversa non è valido: solo perché la derivata in un punto è 0, non è detto che quel punto sia un punto estremante. Vedi il criterio delle derivate successive per saperne di più). In un punto di flesso la derivata seconda è zero. Si possono quindi scoprire tante informazioni sulla tua funzione calcolandone la sua derivata e trovandone gli zeri.