Come si risolvono le equazioni lineari?
Iniziamo con un esempio:
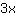
-
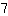
+
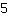
= x +
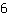
Per prima cosa si procede semplificando entrambi i membri. Nel membro di sinistra
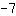
e
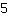
si possono sommare. Si ottiene così l'equazione:
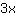
-
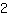
= x +
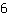
Dopo di che, si riordina l'equazione in modo che l'incognita x è presente solo in uno dei due membri, ad esempio a sinistra, e i termini noti a destra. A destra è presente il termine x. Si possono quindi sotrarre entrambi i membri per x. A sinistra rimane così il termine
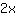
.
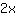
-
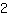
=
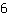
Adesso, si porta il
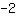
a destra aggiungendo a entrambi i membri
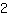
. Cosicché si ha
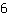
+
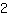
=

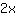
=

Infine, si può dividere entrambi i mebri per il coefficiente dell'incognita x:
x =
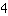
L'equazione è risolta e la soluzione è
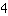
.
Si può procedere sempre nello stesso modo: prima si semplificano il più possibile i membri dell'equazione. Poi si procede semplificando in accordo con i principi di equivalenza: sommare o sottrarre abilmente qualcosa in entrambi i membri. Alla fine si dovrebbe ottenere un multiplo dell'incognita in un membro e un termine noto nell'altro. Dividendo per il coefficiente della variabile, si risolve l'equazione.
Come mostra Mathepower le soluzioni?
Una volta inserita la tua equazione, ottieni:
| Il tuo esercizio: | | Spiegazione dei passaggi: |
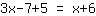 | | | Sommiamo 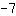 a a 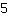 |
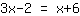 | | | 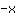 |
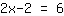 | | | +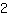 |
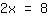 | | | : 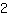 |
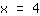 | | |
Insieme delle soluzioni: {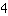 } } |
E se volessi farmi risolvere un'altra equazione?
mathepower.com è qui per questo. Inserisci semplicemente la tua equazione qui sopra e sarà risolta in maniera analoga. Subito e gratuitamente (Mathepower si finanzia tramite pubblicità)
Che casi particolari devono essere presi in considerazione quando si risolvono delle equazioni?
I casi particolari più importanti sono quando l'equazione ha infinite soluzioni (indeterminata) o non ne ha alcuna (impossibile)
Vediamo prima il caso di un'equazione indeterminata:
| Il tuo esercizio: | | Spiegazione dei passaggi: |
 | | | Si espande 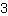 e e 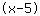 . . |
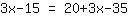 | | | Sommiamo 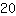 a a 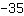 |
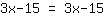 | | | 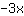 |
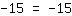 | | | | L'equazione è indeterminata, esistono infinite soluzioni. |
|
Insieme delle soluzioni: R |
Come si può vedere, lo stesso valore è presente in entrambi i mebri, che è sempre vero indipendentemente dal valore della x (la x non è neanche più presente nell'equazione) In questo modo si vede come un'quazione è sempre verificata, ha cioè un numero infinito di soluzioni.
Cosa significa esattamente che l'equazione ha un infinito numero di soluzioni? Basta fare un tentativo: si sostituisca un numero (ad es.
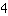
all'interno dell'equazione e si osservi come si ottiene lo stesso valore in entrambi i membri. Questo è valido per ogni valore dato ad x. Il motivo è che i due membri hanno termini equivalenti, cioè termini che danno sempre un risultato uguale per ogni valore di x.
L'altro caso particolare è quello di un'equazione impossibile:
| Il tuo esercizio: | | Spiegazione dei passaggi: |
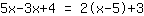 | | | Sommiamo 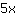 a a 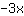 |
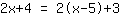 | | | Si espande 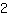 e e 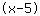 . . |
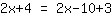 | | |
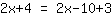 | | | Sommiamo 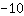 a a 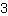 |
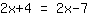 | | | 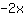 |
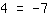 | | | | L'equazione è impossibile, non ha alcuna soluzione. |
|
Insieme delle soluzioni: {} |
Si può qui notare come, dopo aver semplificato e riorganizzato l'equazione, l'incognita x è scomparsa e l'equivalenza rimasta è chiaramente falsa. Questo è dovuto al fatto che già l'equazione di partenza non aveva alcuna soluzione.