बुनियादी रैखिक समीकरण कैसे हल करें?
सबसे पहले, इस उदाहरण को देखें:
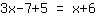
सबसे पहले, दोनों पक्षों पर सरलीकृत करें। बाईं ओर आप
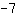
और
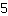
जोड़ सकते हैं। फिर आपको समीकरण मिलेगा:
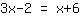
अगला, आपको समीकरण को इस तरह से पुनर्व्यवस्थित करना होगा कि x बाईं ओर और दाईं ओर संख्याएँ हों। चूंकि हमें दाईं ओर x पसंद नहीं है, इसलिए हम दोनों तरफ x को घटाते हैं।
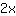
बाईं ओर बाईं ओर है।
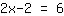
अब, हमें दूसरी तरफ नंबर
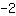
प्राप्त करना है। तो हम कॉटेज पक्षों पर

जोड़ते हैं। चूंकि
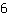
+

=

, हमें मिलता है
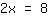
अब, हम दोनों पक्षों को x के सामने संख्या से विभाजित करते हैं:
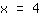
समीकरण अब हल हो गया है;
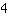
इसका एक समाधान है।
ठीक उसी तरीके से आप हमेशा आगे बढ़ सकते हैं: सबसे पहले, जहाँ तक संभव हो समीकरण के दोनों पक्षों को सरल बनाएं। फिर, समतुल्य परिवर्तनों के साथ सरलीकरण करें। दोनों तरफ से चतुराई से संख्या घटाएं अंत में, एक तरफ एक से अधिक चर और दूसरी तरफ एक संख्या होनी चाहिए। आप चर के सामने संख्या से विभाजित करते हैं और समीकरण हल हो जाता है।
मैथपावर समाधान कैसे दिखाता है?
जब आप एक समीकरण दर्ज करते हैं, तो आपको यह मिलता है:
| आपका अभ्यास: | | क्रमशः: |
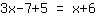 | | | जोड़ना 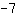 से से 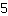 |
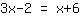 | | | 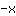 |
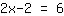 | | | + |
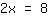 | | | :  |
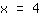 | | |
समाधान सेट: {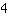 } } |
और अगर मैं एक और समीकरण हल करना चाहता हूं?
आप mathepower.com पर हैं। अपने समीकरण को ऊपर दर्ज करें और इसे उसी प्रक्रिया में हल किया जाएगा। अभी और मुफ्त में (विज्ञापन द्वारा वित्त-पोषण किया जाता है)।
समीकरणों को हल करते समय किन विशेष मामलों पर विचार किया जाना है?
सबसे महत्वपूर्ण विशेष मामलों में समीकरणों की एक अनंत संख्या या समाधान नहीं हैं।
सबसे पहले, समाधान की अनंत संख्या के साथ समीकरण का एक उदाहरण:
| आपका अभ्यास: | | क्रमशः: |
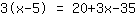 | | | विस्तार 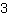 तथा तथा 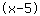 . . |
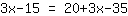 | | | जोड़ना 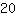 से से 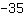 |
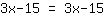 | | | 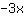 |
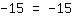 | | | | समीकरण सार्वभौमिक रूप से मान्य है। |
|
समाधान सेट: R |
आप देखते हैं कि आप दोनों तरफ समान संख्याओं के साथ समाप्त होते हैं। यह स्पष्ट रूप से एक्स के किसी भी मूल्य के लिए एक सच्चा बयान है (अब इस समीकरण में कोई एक्स नहीं है)। इस प्रकार, हम देखते हैं कि एक समीकरण में अनंत संख्या में समाधान हो सकते हैं।
इसका क्या मतलब है जब एक समीकरण को अनंत संख्या में समाधान मिले हैं? आप इसे आज़मा सकते हैं: x (जैसे
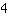
के लिए कोई भी मान लें, दोनों पक्ष समान होंगे। यह x के लिए किसी भी मूल्य के साथ काम करता है। कारण यह है, कि दोनों पक्षों की शर्तें समान हैं, यानी x के लिए किसी भी मान के साथ एक ही समाधान के साथ शब्द।
अन्य विशेष मामला बिना हल के एक समीकरण है:
| आपका अभ्यास: | | क्रमशः: |
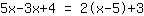 | | | जोड़ना 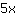 से से 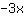 |
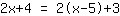 | | | विस्तार  तथा तथा 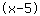 . . |
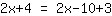 | | |
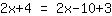 | | | जोड़ना 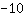 से से 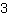 |
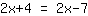 | | |  |
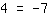 | | | | समीकरण का कोई हल नहीं है। |
|
समाधान सेट: {} |
हम देखते हैं कि पुन: व्यवस्थित करने के बाद समीकरण में कोई x नहीं है और समीकरण स्पष्ट रूप से गलत है। यह मूल समीकरण का कोई समाधान नहीं होने के कारण है।