How to solve basic linear equations?
First, take a look at this example:
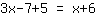
First, simplify on boths sides. On the left side you can add
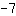
and
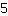
. Then you get the equation:
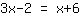
Next, you have to rearrange the equation in such a way that x is on the left side and numbers on the right side. Since we don't like the x on the right side, we substract x on both sides.
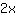
are left on the left side.
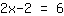
Now, we have to get the number

on the other side. So we add
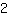
on bothe sides. Since
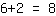
, we get
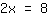
Now, we divide both sides by the number in front of the x:
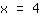
The equation is solved now;
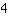
is a solution of it.
In the exact same manner you can always proceed: First, simplify both sides of the equation as far as possible. Then, simplify with equivalence transformations. Subtract a number cleverly on both sides Finally, there should be a multiple of the variables on one sode and a number on the other side. You divide by the number in front of the variable and the equation is solved.
How does Mathepower show solutions?
When you've entered an equation, you get this:
| Your exercise: | | Step by step: |
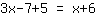 | | | add 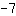 to to 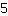 |
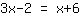 | | | 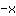 |
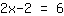 | | | +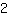 |
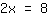 | | | : 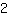 |
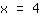 | | |
Solution set: {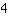 } } |
And if I want to have another equation being solved?
You are on mathepower.com. Enter your equation above and it will be solved in the same procedure. Right now and for free (mathepower is financed by advertising).
What special cases have to be considered when solving equations?
The most important special cases are equation having an infinite number of solutions or no solution.
First, an example of an equation with an infinite number of solutions:
| Your exercise: | | Step by step: |
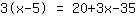 | | | Expand 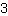 and and 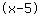 . . |
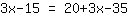 | | | add 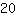 to to 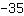 |
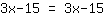 | | | 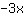 |
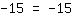 | | | | The equation is universally valid. |
|
Solution set: R |
You see that you end up with the same numbers on both side. It's obviously a true statement for any value of x (there is no x in this equation anymore). Thus, we see that an equation can have an infinite number of solutiosn.
What does it mean when an equation has got an infinite number of solutions? You can try it out: Take any value for x (e.g.
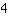
, both sides will be the same. It works with any value for x. The reason is, that the terms on both sides are equivalent, i.e. terms with the same solution with any value for x.
The other special case is an equation with no solution:
| Your exercise: | | Step by step: |
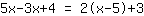 | | | add 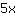 to to 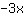 |
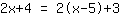 | | | Expand 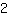 and and 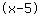 . . |
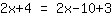 | | |
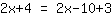 | | | add 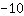 to to 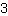 |
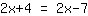 | | |  |
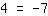 | | | | The equation has no solutions. |
|
Solution set: {} |
We see that there is no x in the equation after rearranging and that the equation is obviously false. This is due to the original equation having no solution.