What does curve sketching mean?
Curve sketching is a calculation to find all the characteristic points of a function, e.g. roots, y-axis-intercept, maximum and minimum turning points, inflection points.
How to get those points?
By calculating derivatives. Then you set the function as well as the derivative equal to zero: Roots are solutions of the equation
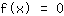
. Turning points can be at the roots of the derivation, i.e. you gotta solve the equation
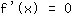
for finding maximum / minimum turning points. (if of if not there is a turning point at the root of the derivation, can be checked by using the change of sign criterion.) At an inflection point, the second derivation has to be

, so to find inflection points solve the equation
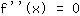
.
Why is curve skething done less nowadays?
It is a bit stupid: You just have to learn a way to do the same point calculations every time without thinking too much about their meaning. Therefore, exercises where you have to think about the meaning of those points become more important nowadays.
Can I take a look at an example?
Of course. Lets sketch the curve
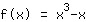
.
Mathepower works with this function:
This is the graph of your function.
|
|
- Roots at -1; 0; 1
- y-axis intercept at (0|0)
- Maximum and minimum turning points at (-0.577|0.385); (0.577|-0.385)
- Inflection points at (0|0)
This is what Mathepower calculated:
Roots:
Looking for roots of 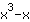
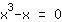 | | | Factor out 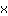 . . |
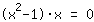 | | | 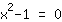 | | | The product equals 0. So either the factor 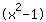 must be zero…. must be zero…. |
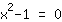 | | | +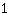 |
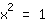 | | | Take the square root on both sides. |
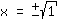 | | | 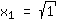 | | | Extract the root of 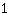 |
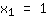 | | | 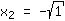 | | | Extract the root of 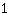 |
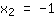 | | | 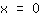 | | | … or the factor 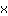 must be zero must be zero |
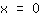 | | |
So, the roots are: {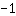 ; ; ; ;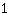 } }
Symmetry:
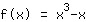 is point symmetric to the origin. is point symmetric to the origin.
Calculate the y-axis intercept by inserting 0.
Insert 0 into the function 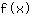 : :
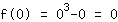
So, the y-axis intercept is at (0|0)
Diffentiate the function 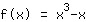
| Differentiate the function 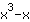 : : | ( Derivative of  ) ) | + | ( Derivative of 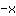 ) ) | 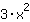 | + | 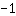 |
So, the derivative of 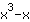 is is 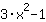 . . |
| |
|
So the first derivative is 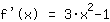
Second derivative, i.e. derivative of 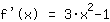 : :
| Differentiate the function 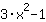 : : | ( Derivative of 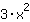 ) ) | + | ( Derivative of 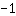 ) ) | 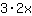 | + |  |
So, the derivative of 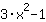 is is 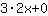 . . |
| |
|
Simplify the differentiation:
So the second derivative is 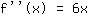
Third derivative, i.e. derivative of 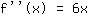 : :
The derivative of 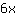 is is 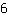
So the third derivative is 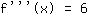
Looking for turning points.
We have to find roots of the first derivative.
Looking for roots of 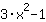
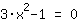 | | | +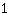 |
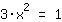 | | | : 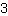 |
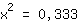 | | | Take the square root on both sides. |
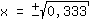 | | | 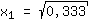 | | | Extract the root of  |
 | | | 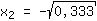 | | | Extract the root of  |
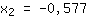 | | |
Turning points could be at {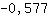 ; ;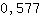 } }
Insert the roots of the first derivative into the second derivative:
Insert -0.577 into the function 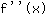 : :
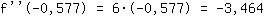
-3.464 is less than 0. So there is a maximum at 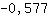 . .
Insert -0.577 into the function 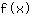 : :
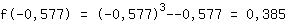
Maximum turning point (-0.577|0.385)
Insert 0.577 into the function 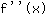 : :

3.464 is larger than 0. So there is a mimimum at 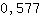 . .
Insert 0.577 into the function 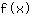 : :
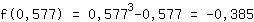
Minimum turning point (0.577|-0.385)
Looking for inflection points.
We have to find roots of the second derivative.
Looking for roots of 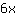
Inflection points could be at { } }
Insert the roots of the second derivative into the third derivative:
The third derivative does not contain x , so insertion gives 6
6 is larger than 0, so there is an inflection point at  . .
Insert 0 into the function 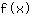 : :
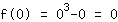
Inflection point (0|0)
|