What is a power function
A power function is a function of the form
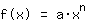
. This means it just consists of a number a and a power
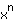
.
What should I know about its symmetry?
Symmetry of power functions is simple: If the power is even, the graph of the power function is axis symmetric to the y-axis. Example:
The powers are all even, therefore the power functions are axis symmetric to the y-axis.
On the other hand, all graphs of power functions with odd exponent are point symmetric to the origin:
The powers are all odd, so the power functions are point symmetric to the origin.
Why are power functions that important?
Most functions learned at school are polynomial functions. Polynomial functions are the sum of power functions.