What is a linear function?
A linear function is a function whose graph is a line. The general form of a linear function is
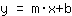
, where m is the slope and b is the y-axis intercept. Here is an example:
Your exercise: 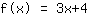
This is the graph of your function.
|
|
- Roots at -1.333
- y-axis intercept at (0|4)
|
The graph of a linear function is always a line.
A similar word to linear function is linear correlation.
What is the slope of a linear function?
The slope of a linear function corresponds to the number in front of the x. It says how may units you have to go up / down if you go one unit to the right. Example:
Your exercise: 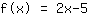
This is the graph of your function.
|
|
- Roots at 2.5
- y-axis intercept at (0|-5)
|
We see that this function has slope
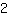
. If we go one square to the right of any point on the graph, we have to go two squares up to be on the graph again.
Another example, this time with negative slope:
Your exercise: 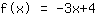
This is the graph of your function.
|
|
- Roots at 1.333
- y-axis intercept at (0|4)
|
This linear function has slope
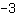
. This means whenever we go one square to the right, we have to go three squares down to be on the graph again.
What is the y-line intercept of a linear function?
The y-line intercept is the number at the end of the function. As the name says, it says where the function cuts the y-axis. If you take a look on the function graphs, you see that
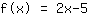
intersects the y-axis at

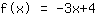
intersects the y-axis at
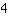
.
How to calculate the equation of the line from a point and the slope?
You have to insert the point into the equation, i.e. the one coordinate for x and the other one for f(x). Here is an example: Lets assume we know that our function has slope
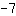
and goes through (-2|5).
Your exercise:
Point (-2|5); Slope -7;
Your exercise: 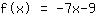
This is the graph of your function.
|
|
- Roots at -1.286
- y-axis intercept at (0|-9)
This is what Mathepower calculated:
Calculate the y-axis intercept b by inserting:
General form of the linear function: f(x)=mx+b
Insert 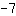 for m, for m,  for x and for x and 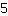 for f(x). for f(x).
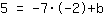 | | | Multiply 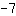 by by  |
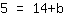 | | | Swap both sides of the equation. |
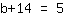 | | | 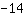 |
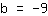 | | |
So, the y-axis intercept is at 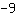
Therefore, the equation of the function is 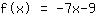
|
How to calculate the equation of a linear function from two given points?
First, we have to calculate the slope m by inserting the x- and y- coordinates of the points into the formula
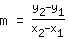
. This means: You calculate the difference of the y-coordinates and divide it by the difference of the x-coordinates. Here is an example:
Your exercise:
Point (1|2); Point (3|8);
Your exercise: 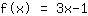
This is the graph of your function.
|
|
- Roots at 0.333
- y-axis intercept at (0|-1)
This is what Mathepower calculated:
To calculate the slope m, use the formula 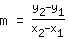 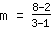 | | | add  to to  |
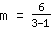 | | | add 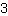 to to 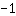 |
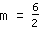 | | | Divide 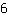 by by 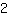 |
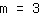 | | |
Calculate the y-axis intercept b by inserting:
General form of the linear function: f(x)=mx+b
Insert 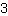 for m, for m, 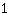 for x and for x and 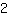 for f(x). for f(x).
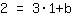 | | |
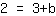 | | | Swap both sides of the equation. |
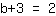 | | | 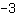 |
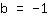 | | |
So, the y-axis intercept is at 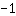
Therefore, the equation of the function is 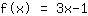
|
As we can see, the slope was calculated first. To find the equation of the function, you have to insert a point and get an equation which gives the y-axis intercept.
Can I see more examples?
Of course. Just enter you own examples above and they will be calculated immediately step-by-step. (This is the idea of Mathepower:
You don't just look at some already done explanations, but you get your own calculations explained!)