The following formulas are right in equations:
Sine rule:
a / b = sin alpha / sin beta
Cosine rule:
a^2=b^2+c^2-2bc cos alpha
Triangles
What is a triangle?
Here we can see a triangle.
A triangle has three sides and three corners.
In every corner, there is an interior angle, i.e. the angle between the sides ending at that corner.
The sum of all interior angles of a triangle is always 180 degrees.
By what information is a triangle uniquely determined?
A triangle is always determined by its three side lengths. It is also determined by two angles and one side, ord by two sides and the angle between those sides.
A triangle can also be determined by three other values. But for example, if you got two sides and the height on one side, there is more than one possible triangle with those lengths.
What is the height of a triangle?
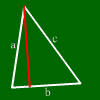
The height is the distance beween one side and the opposing corner.
What calculations can be done in a triangle?
The area can be calculated as (side*height)/2 for any side and the corresponding height.
The sides and angles can be calculated by using sine and cosine. The following formulae hold:
a/sin(alpha)=b/sin(beta) (sine rule)
Furthermore, for three sides a,b,c and angle alpha opposing of a:
a^2=b^2+c^2-2bc cos alpha (cosine rule)
What interesting lines exist on triangles?
Interesting lines are the perpendicular bisectors, the angle bisectors, the median lines
and the heights.
What special cases are interesting?
Interesting special cases are the isosceles triangle, the
equilateral triangle and the right-angled triangle.
For further information, move the mouse above the words below and the corresponding line will be marked on the triangle.
Side a
Side b
Side c
Angle alpha
Angle beta
Angle gamma
height on a
height on b
height on c
median line on a
median line on b
median line on c
angle bisector of alpha
angle bisector of beta
angle bisector of gamma
area