Finding functions


Find a function

Degree of the function:
1 2 3 4 5

( The degree is the highest power of an x. )


Symmetries:
axis symmetric to the y-axis
point symmetric to the origin


y-axis intercept



Roots / Maxima / Minima /Inflection points:
at x=
at x=
at x=
at x=
at x=


Characteristic points:
at |)
at |)
at |)
at (|)
at (|)


Slope at given x-coordinates:
Slope at x=
Slope at x=
Slope at

What's this about?

This is, in some way, the opposite of curve sketching. Curve sketching means you got a function and are looking for roots, turning and inflection points. What we do here is the opposite: Your got some roots, inflection points, turning points etc. and are looking for a function having those.

How to reconstruct a function?

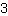
Primarily, you have to find equations and solve them. This gives you the coefficients of your function. Here is an example: Let's assume we are looking for a function of degree 3 having a minimum turning point at (1|-4) and a maximum turning point at (-1|3).


You are looking for a function with:
quadratic function
Maximum turning point at (-1|3)
Minimum turning point at (1|-4)

Mathepower found the following function:
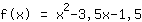
1*f(x)=1*x^2+-3.5*x+-1.5
This is the graph of your function.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Roots at -0.386; 3.886
  • y-axis intercept at (0|-1.5)
  • Maximum and minimum turning points at (1.75|-4.563)
  • Inflection points

This is how Mathepower calculated:
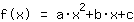
f(x)=1*a*x^2+1*b*x+1*c
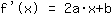
f'(x)=2*a*x+1*b
f''(x)=2*a

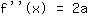
The point at (-1|3) gives the equation :
f(-1)=3
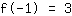
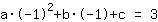
1*a*-1^2+1*b*-1+1*c=3
simplified: :
1a-1b+1c=3

The point at (1|-4) gives the equation :
f(1)=-4
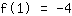
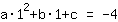
1*a*1^2+1*b*1+1*c=-4
simplified: :
1a+1b+1c=-4

So, we got the following system of equations: :
  a   -1b   +c    = 3 
  a   +b   +c    = -4 

This is how to solve this system of equations:
  a   -1b   +c    = 3 
  a   +b   +c    = -4 
  a   -1b   +c    = 3 
     2b       = -7 
 ( -1 times line 1 was added to line 2 )
  a   -1b   +c    = 3 
     b       = -3,5 
 ( The 2 line was divided by 2 )

2 line: b+0c = -3,5
c can be chosen freely
Solve for b : :   b = 0c -3,5

1 line:
a  -1b  +c   =  3
Substitute variables already known:   
a  -1⋅(0c -3,5)  +⋅1c    =  3
Solve for a : a = -1c -0,5
Set a equal to
This means that c is equal to -1,5

Inserting shows that the function equals to 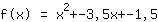f(x)=1*1*x^2+1*-3.5*x+1*-1.5 ist.



How to find a function through given points?

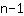
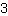
The general rule is that for any n given points there is a function of degree n-1 whose graph goes through them. So e.g. you find by solving equations a function of degree 3 through the four points (-1|3), (0|2), (1|1) und (2|4):


You are looking for a function with:
Function of degree 3
Point at (-1|3)
Point at (0|2)
Point at (1|1)
Point at (2|4)

Mathepower found the following function:
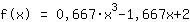
1*f(x)=0.667*x^3+-1.667*x+2
This is the graph of your function.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Roots at -2
  • y-axis intercept at (0|2)
  • Maximum and minimum turning points at (-0.913|3.014); (0.913|0.986)
  • Inflection points at (0|2)

This is how Mathepower calculated:
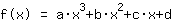
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
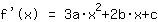
f'(x)=3*a*x^2+2*b*x+1*c
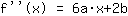
f''(x)=6*a*x+2*b

The point at (-1|3) gives the equation :
f(-1)=3
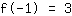
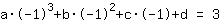
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
simplified: :
-1a+1b-1c+1d=3

The point at (0|2) gives the equation :
f(0)=2
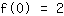
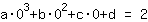
1*a*0^3+1*b*0^2+1*c*0+1*d=2
simplified: :
0a+0b+0c+1d=2

The point at (1|1) gives the equation :
f(1)=1
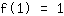
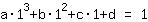
1*a*1^3+1*b*1^2+1*c*1+1*d=1
simplified: :
1a+1b+1c+1d=1

The point at (2|4) gives the equation :
f(2)=4
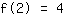
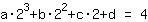
1*a*2^3+1*b*2^2+1*c*2+1*d=4
simplified: :
8a+4b+2c+1d=4

So, we got the following system of equations: :
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 

This is how to solve this system of equations:
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
     -4b   -6c   -7d    = -4 
 ( -8 times line 3 was added to line 4 )
  -1a   +b   -1c   +d    = 3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( 1 times line 1 was added to line 3 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( The 1 line was divided by -1 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
        -6c   -3d    = 4 
 ( 2 times line 3 was added to line 4 )
  a   -1b   +c   -1d    = -3 
     2b      +2d    = 4 
           d    = 2 
        -6c   -3d    = 4 
 ( the 3 line was interchanged with the 2 line )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
           d    = 2 
        -6c   -3d    = 4 
 ( The 2 line was divided by 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        -6c   -3d    = 4 
           d    = 2 
 ( the 4 line was interchanged with the 3 line )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        c   +0,5d    = -0,667 
           d    = 2 
 ( The 3 line was divided by -6 )


4 line:
      d   =  2

3 line:
    c  +0,5d   =  -0,667
Substitute variables already known:   
    c  +0,5⋅2   =  -0,667
Solve for c : c = -1,667

2 line:
  b    +d   =  2
Substitute variables already known:   
  b    +⋅2   =  2
Solve for b : b = 0

1 line:
a  -1b  +c  -1d   =  -3
Substitute variables already known:   
a  -1⋅0  +⋅(-1,667)  -1⋅2   =  -3
Solve for a : a = 0,667

Inserting shows that the function equals to 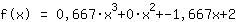f(x)=1*0.667*x^3+1*0*x^2+1*-1.667*x+1*2 ist.



How to find a function with a given inflection point?

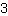
An inflection point gives multiple equations: On the one hand, you got the y-value. On the other hand, you know that the second derivative is 0 at an inflection point. Let's take a look at an example for a function of degree 3 having an inflection point at (1|3):


You are looking for a function with:
Function of degree 3
root at 2
root at 4
Inflection point at (1|3)

Mathepower found the following function:
1*f(x)=1*c*x+1*d
This is the graph of your function.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Roots
  • y-axis intercept at (0|0)
  • Maximum and minimum turning points
  • Inflection points

This is how Mathepower calculated:
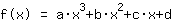
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
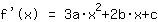
f'(x)=3*a*x^2+2*b*x+1*c
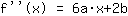
f''(x)=6*a*x+2*b

The point at (1|3) gives the equation :
f(1)=3
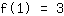
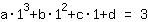
1*a*1^3+1*b*1^2+1*c*1+1*d=3
simplified: :
1a+1b+1c+1d=3

So, we got the following system of equations: :
  a   +b   +c   +d    = 3 

This is how to solve this system of equations:
  a   +b   +c   +d    = 3 

1 line: c+1d = 3
d can be chosen freely
Solve for c : :   c = -1d +3

Inserting shows that the function equals to 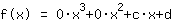f(x)=1*0*x^3+1*0*x^2+1*c*x+1*d ist.



And how to use that in my example?

Just enter your exercise above. Mathepower shows how it works by doing a free step-by-step calculation. Or just make up any interesting exercise and check out what Mathepower does.