Étude graphique de fonctions


On cherche la fonction

Degré de la fonction:
1 2 3 4 5

( Le degré est la puissance la plus élevée de la x. )


Symétries:
symétrique à l'axe y
symétrique à l'origine


Ordonnée à l'origine



Racines / Maximums / Minimums / Points d'inflexion:
à x=
à x=
à x=
à x=
à x=


Points caractéristiques:
à |)
à |)
à |)
à (|)
à (|)


Pente dans le points:
Pente à x=
Pente à x=
Pente à

C'est à propos de quoi?

L'étude du graphique d'une fonction est l'opposé de l'étude de fonction. Ce dernier signifie que vous avez une fonction et que vous cherchez les racines, les points stationnaires, tournants et d'inflexion, et critiques. Ce que nous faisons dans l'étude d'un graphique est le contraire, c'est-à-dire obtenir la fonction ayant donnés les paramètres de sa représentation graphique:

Comment étudier le graphique une fonction?

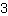
Vous devez principalement trouver des équations et les résoudre. Cela vous donne les coefficients de votre fonction. Voici un exemple: Supposons que nous recherchons une fonction de degré 3 ayant un point tournant minimal à (1|-4) et un point tournant maximal à (-1|3).


Vous recherchez une fonction avec:
fonction quadratique
Point tournant maximal à (-1|3)
Point tournant minimal à (1|-4)

Mathepower a trouvé la fonction suivante:
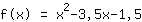
1*f(x)=1*x^2+-3.5*x+-1.5
Ceci est le graphique de votre fonction.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Racines à -0.386; 3.886
  • Ordonnée à l'origine à (0|-1.5)
  • Points tournants maximal/minimal à (1.75|-4.563)
  • Points d'inflexion

Mathepower a calculé comme suit:
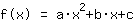
f(x)=1*a*x^2+1*b*x+1*c
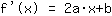
f'(x)=2*a*x+1*b
f''(x)=2*a

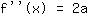
Le point (-1|3) donne l'équation :
f(-1)=3
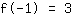
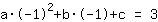
1*a*-1^2+1*b*-1+1*c=3
simplifiée: :
1a-1b+1c=3

Le point (1|-4) donne l'équation :
f(1)=-4
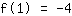
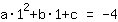
1*a*1^2+1*b*1+1*c=-4
simplifiée: :
1a+1b+1c=-4

Nous avons donc obtenu le système d'équations suivant: :
  a   -1b   +c    = 3 
  a   +b   +c    = -4 

Voici comment résoudre ce système d'équations:
  a   -1b   +c    = 3 
  a   +b   +c    = -4 
  a   -1b   +c    = 3 
     2b       = -7 
 ( -1 fois l'équation 1 a été ajouté à l'équation 2 )
  a   -1b   +c    = 3 
     b       = -3,5 
 ( l'équation 2 a été divisée par 2 )

2 ° équation: b+0c = -3,5
c peut être choisi librement
Résoudre pour b : :   b = 0c -3,5

1 ° équation:
a  -1b  +c   =  3
On substitue les variables déjà calculées:   
a  -1⋅(0c -3,5)  +⋅1c    =  3
Résoudre pour a : a = -1c -0,5
On met a égal à 1.
Cela signifie que c est égal à -1,5

La substitution montre que la fonction est égale à 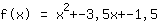f(x)=1*1*x^2+1*-3.5*x+1*-1.5 ist.



Comment trouver une fonction à travers des points donnés?

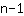
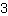
La règle générale est que pour tout n points donnés, il existe une fonction de degré n-1 dont le graphe les parcourt. Donc par exemple il existe toujours une fonction du degré 3 qui passe à travers des quatre points (-1|3), (0|2), (1|1) et (2|4):


Vous recherchez une fonction avec:
fonction de degré 3
Le point à (-1|3)
Le point à (0|2)
Le point à (1|1)
Le point à (2|4)

Mathepower a trouvé la fonction suivante:
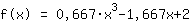
1*f(x)=0.667*x^3+-1.667*x+2
Ceci est le graphique de votre fonction.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Racines à -2
  • Ordonnée à l'origine à (0|2)
  • Points tournants maximal/minimal à (-0.913|3.014); (0.913|0.986)
  • Points d'inflexion à (0|2)

Mathepower a calculé comme suit:
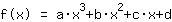
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
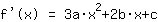
f'(x)=3*a*x^2+2*b*x+1*c
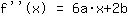
f''(x)=6*a*x+2*b

Le point (-1|3) donne l'équation :
f(-1)=3
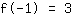
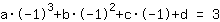
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
simplifiée: :
-1a+1b-1c+1d=3

Le point (0|2) donne l'équation :
f(0)=2
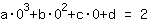
1*a*0^3+1*b*0^2+1*c*0+1*d=2
simplifiée: :
0a+0b+0c+1d=2

Le point (1|1) donne l'équation :
f(1)=1
1*a*1^3+1*b*1^2+1*c*1+1*d=1
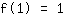
simplifiée: :
1a+1b+1c+1d=1

Le point (2|4) donne l'équation :
f(2)=4
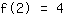
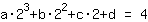
1*a*2^3+1*b*2^2+1*c*2+1*d=4
simplifiée: :
8a+4b+2c+1d=4

Nous avons donc obtenu le système d'équations suivant: :
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 

Voici comment résoudre ce système d'équations:
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
     -4b   -6c   -7d    = -4 
 ( -8 fois l'équation 3 a été ajouté à l'équation 4 )
  -1a   +b   -1c   +d    = 3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( 1 fois l'équation 1 a été ajouté à l'équation 3 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( l'équation 1 a été divisée par -1 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
        -6c   -3d    = 4 
 ( 2 fois l'équation 3 a été ajouté à l'équation 4 )
  a   -1b   +c   -1d    = -3 
     2b      +2d    = 4 
           d    = 2 
        -6c   -3d    = 4 
 ( l'équation 3 a été substituée avec l'équation 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
           d    = 2 
        -6c   -3d    = 4 
 ( l'équation 2 a été divisée par 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        -6c   -3d    = 4 
           d    = 2 
 ( l'équation 4 a été substituée avec l'équation 3 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        c   +0,5d    = -0,667 
           d    = 2 
 ( l'équation 3 a été divisée par -6 )


4 ° équation:
      d   =  2

3 ° équation:
    c  +0,5d   =  -0,667
On substitue les variables déjà calculées:   
    c  +0,5⋅2   =  -0,667
Résoudre pour c : c = -1,667

2 ° équation:
  b    +d   =  2
On substitue les variables déjà calculées:   
  b    +⋅2   =  2
Résoudre pour b : b = 0

1 ° équation:
a  -1b  +c  -1d   =  -3
On substitue les variables déjà calculées:   
a  -1⋅0  +⋅(-1,667)  -1⋅2   =  -3
Résoudre pour a : a = 0,667

La substitution montre que la fonction est égale à 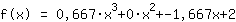f(x)=1*0.667*x^3+1*0*x^2+1*-1.667*x+1*2 ist.



Comment trouver une fonction à travers un point d'inflexion?

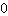
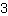
Un point d'inflexion donne plusieurs équations: d'une part on a l'appartenance du point à la fonction, d'un autre côté l'appartenance à la dérivée première, la condition pour laquelle la dérivée seconde est 0 à un point d'inflexion. Prenons un exemple d'une fonction de degré 3 ayant un point d'inflexion à (1|3):


Vous recherchez une fonction avec:
fonction de degré 3
Racine à 2
Racine à 4
Point d'inflexion oblique à (1|3)

Mathepower a trouvé la fonction suivante:
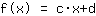
1*f(x)=1*c*x+1*d
Ceci est le graphique de votre fonction.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Racines
  • Ordonnée à l'origine à (0|0)
  • Points tournants maximal/minimal
  • Points d'inflexion

Mathepower a calculé comme suit:
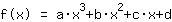
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
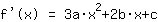
f'(x)=3*a*x^2+2*b*x+1*c
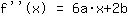
f''(x)=6*a*x+2*b

Le point (1|3) donne l'équation :
f(1)=3
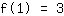
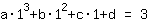
1*a*1^3+1*b*1^2+1*c*1+1*d=3
simplifiée: :
1a+1b+1c+1d=3

Nous avons donc obtenu le système d'équations suivant: :
  a   +b   +c   +d    = 3 

Voici comment résoudre ce système d'équations:
  a   +b   +c   +d    = 3 

1 ° équation: c+1d = 3
d peut être choisi librement
Résoudre pour c : :   c = -1d +3

La substitution montre que la fonction est égale à 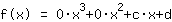f(x)=1*0*x^3+1*0*x^2+1*c*x+1*d ist.



Et comment utiliser cela dans mon exercice?

Entrez simplement votre exercice ci-dessus, Mathepower vous montre comment le résoudre, ou tout simplement inventez-le et observez son résultat.