函数方程确定


函数查找

函数的次数：
1 2 3 4 5

( 次数 即是未知数 x 的最高次幂。 )


对称性：
关于 y-轴 轴对称
关于 原点 点对称


y-轴截距



零点 / 极值点 / 拐点
在 x=
在 x=
在 x=
在 x=
在 x=


特征点：
在 |)
在 |)
在 |)
在 (|)
在 (|)


点处斜率：
斜率 在 x=
斜率 在 x=
斜率 在

这是关于什么的？

在某些方面，这是函数图像绘制的相反面。图像绘制意味着，我们有了一个函数，然后寻找 零点、极值和拐点。在这里，我们进行相反的操作： 我们已知了一些零点、极值和拐点等，然后来求有这些值的函数方程。

如何重组一个函数？

首先，我们要找到一些等量关系，并求解。从而得到函数的系数。这里有一个例子： 假设我们要寻找一个三次函数，最小极值点在 (1|-4) ，最大极值点在 (-1|3)。


寻找有以下特征的函数：
二次函数
最大极值点 在 (-1|3)
最小极值点 在 (1|-4)

Mathepower找到了以下的函数：
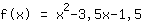
1*f(x)=1*x^2+-3.5*x+-1.5
这是方程的图像
Dein Browser untersttzt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • 零点 在 -0.386; 3.886
  • y-轴截距 在 (0|-1.5)
  • 最大和最小极值点 在 (1.75|-4.563)
  • 拐点

Mathepower是这样计算的：
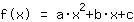
f(x)=1*a*x^2+1*b*x+1*c
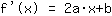
f'(x)=2*a*x+1*b
f''(x)=2*a

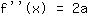
点在 (-1|3) 得到等式 :
f(-1)=3
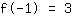
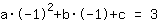
1*a*-1^2+1*b*-1+1*c=3
简化： :
1a-1b+1c=3

点在 (1|-4) 得到等式 :
f(1)=-4
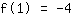
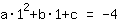
1*a*1^2+1*b*1+1*c=-4
简化： :
1a+1b+1c=-4

所以得到方程组： :
  a   -1b   +c    = 3 
  a   +b   +c    = -4 

方程组解法：
  a   -1b   +c    = 3 
  a   +b   +c    = -4 
  a   -1b   +c    = 3 
     2b       = -7 
 ( 此 -1 倍行 1 与行 2 相加。 )
  a   -1b   +c    = 3 
     b       = -3,5 
 ( 此 2 行将除以 2 )

2 行： b+0c = -3,5
c 可任意选择
对 b 求解： :   b = 0c -3,5

1 行：
a  -1b  +c   =  3
代入已知参数   
a  -1⋅(0c -3,5)  +⋅1c    =  3
对 a 求解： a = -1c -0,5
将 a 等于1.
意味着 c 等于 -1,5

输入得到，函数等于 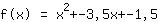f(x)=1*1*x^2+1*-3.5*x+1*-1.5 ist.



如何通过这些点来找到函数呢？

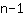
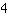
通常的规则是：对于给出的任意 n 个点，可以确定一个 n-1 次的函数，其函数图像通过这些点。所以，例如通过解方程 可以将经过 4 个点 (-1|3), (0|2), (1|1) 和 (2|4) 的 3次函数确定下来：


寻找有以下特征的函数：
函数的次数 3
点 在 (-1|3)
点 在 (0|2)
点 在 (1|1)
点 在 (2|4)

Mathepower找到了以下的函数：
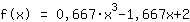
1*f(x)=0.667*x^3+-1.667*x+2
这是方程的图像
Dein Browser untersttzt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • 零点 在 -2
  • y-轴截距 在 (0|2)
  • 最大和最小极值点 在 (-0.913|3.014); (0.913|0.986)
  • 拐点 在 (0|2)

Mathepower是这样计算的：
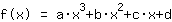
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
f'(x)=3*a*x^2+2*b*x+1*c
f''(x)=6*a*x+2*b

点在 (-1|3) 得到等式 :
f(-1)=3
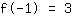
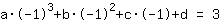
1*a*-1^3+1*b*-1^2+1*c*-1+1*d=3
简化： :
-1a+1b-1c+1d=3

点在 (0|2) 得到等式 :
f(0)=2
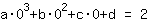
1*a*0^3+1*b*0^2+1*c*0+1*d=2
简化： :
0a+0b+0c+1d=2

点在 (1|1) 得到等式 :
f(1)=1
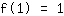
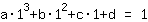
1*a*1^3+1*b*1^2+1*c*1+1*d=1
简化： :
1a+1b+1c+1d=1

点在 (2|4) 得到等式 :
f(2)=4
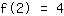
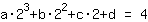
1*a*2^3+1*b*2^2+1*c*2+1*d=4
简化： :
8a+4b+2c+1d=4

所以得到方程组： :
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 

方程组解法：
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
  8a   +4b   +2c   +d    = 4 
  -1a   +b   -1c   +d    = 3 
           d    = 2 
  a   +b   +c   +d    = 1 
     -4b   -6c   -7d    = -4 
 ( 此 -8 倍行 3 与行 4 相加。 )
  -1a   +b   -1c   +d    = 3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( 此 1 倍行 1 与行 3 相加。 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
     -4b   -6c   -7d    = -4 
 ( 此 1 行将除以 -1 )
  a   -1b   +c   -1d    = -3 
           d    = 2 
     2b      +2d    = 4 
        -6c   -3d    = 4 
 ( 此 2 倍行 3 与行 4 相加。 )
  a   -1b   +c   -1d    = -3 
     2b      +2d    = 4 
           d    = 2 
        -6c   -3d    = 4 
 ( 此 3 行将与 2 行调换。 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
           d    = 2 
        -6c   -3d    = 4 
 ( 此 2 行将除以 2 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        -6c   -3d    = 4 
           d    = 2 
 ( 此 4 行将与 3 行调换。 )
  a   -1b   +c   -1d    = -3 
     b      +d    = 2 
        c   +0,5d    = -0,667 
           d    = 2 
 ( 此 3 行将除以 -6 )


4 行：
      d   =  2

3 行：
    c  +0,5d   =  -0,667
代入已知参数   
    c  +0,5⋅2   =  -0,667
对 c 求解： c = -1,667

2 行：
  b    +d   =  2
代入已知参数   
  b    +⋅2   =  2
对 b 求解： b = 0

1 行：
a  -1b  +c  -1d   =  -3
代入已知参数   
a  -1⋅0  +⋅(-1,667)  -1⋅2   =  -3
对 a 求解： a = 0,667

输入得到，函数等于 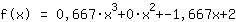f(x)=1*0.667*x^3+1*0*x^2+1*-1.667*x+1*2 ist.



如何通过给出的拐点求函数方程？

根据拐点可以求出许多个方程：一方面我们知道 y-值，另一方面我们知道 在拐点处，二阶导数为 0。让我们看一个例子，一个三次函数，拐点在 (1|3)：


寻找有以下特征的函数：
函数的次数 3
根 在 2
根 在 4
拐点 在 (1|3)

Mathepower找到了以下的函数：
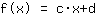
1*f(x)=1*c*x+1*d
这是方程的图像
Dein Browser untersttzt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • 零点
  • y-轴截距 在 (0|0)
  • 最大和最小极值点
  • 拐点

Mathepower是这样计算的：
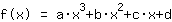
f(x)=1*a*x^3+1*b*x^2+1*c*x+1*d
f'(x)=3*a*x^2+2*b*x+1*c
f''(x)=6*a*x+2*b

点在 (1|3) 得到等式 :
f(1)=3
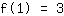
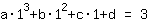
1*a*1^3+1*b*1^2+1*c*1+1*d=3
简化： :
1a+1b+1c+1d=3

所以得到方程组： :
  a   +b   +c   +d    = 3 

方程组解法：
  a   +b   +c   +d    = 3 

1 行： c+1d = 3
d 可任意选择
对 c 求解： :   c = -1d +3

输入得到，函数等于 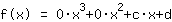f(x)=1*0*x^3+1*0*x^2+1*c*x+1*d ist.



我如何将它们运用在我的习题中呢？

只需要在上方输入你的习题，Mathepower 告诉你如何一步一步地求解计算。或者随便想一些有趣的 习题，看看Mathepower可以做点什么。