Change of signs



Enter your function here.
Hint: Enter as 3*x^2 ,
as 3/5 and
as (x+1)/(x-2x^4)


What is the use of the change of sign?

By checking for the change of sign, you can check whether a function with derivative 0 has a maximum / minimum turning point or a saddle point. Here are three examples where the function has slope 0 in (1|2):

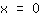
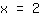
This function has slope 0 in (1|2) and a maximum turning point. At x=0 the graph ascends, i.e. the derivative is larger than 0 in here. At x=2 the Graph falls, i.e. the derivative is less than 0. This means that around a maximum turning point, the sign of the derivative is + before and - after the turning point. This means the derivative changes signs from + to - .



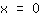
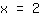
This function has slope 0 in (1|2), but a minimum turning point. At x=0 the graph falls, i.e. the derivation here is less than 0. At x=2 the graph ascends, i.e. the derivation is larger than 0. This implies that at a minimum turning point, the sign of the derivation is - before and + after the turning point. This means the derivation changes signes from - to +.



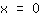
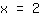
This function also has slope 0 at (1|2), but no turning point. You see that the graph ascends at x=0 as well as at x=2. This implies you have no turning point if the derivation does not change signs. Such a point (that is no turning point but has derivation 0 ) is called saddle point.

How to use the change of sign criterion?

  • First derivate your function.
  • Then calculate the roots of the derivation. Only those roots can be x-coordinates of turning points.
  • Then you insert x-values close to the derivation roots into the derivation. If the derivation changes signs around the derivation, you found a turning point. Otherwise not.

    • Why is change of signs called a sufficient criterium?

    The derivation being 0 is necessary for a turning point (i.e. it is always the case at a turning point). But it is not necessary, what means, just because the derivation is 0, there does not have to be a turning point (check out for the saddle point above).
    If the derivation is not only 0, but also changes signs, then you have to have a turning point. In mathematics, we say that derivation 0 and change of signs is sufficient for having a turning point.

    Can I see an example?

    Of course. This is Mathepower. Just enter your function and get the turning points calculated step by step.