संकेत के परिवर्तन का उपयोग क्या है?
संकेत के परिवर्तन के लिए जाँच करके, आप जाँच सकते हैं कि व्युत्पन्न
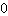
के साथ एक फ़ंक्शन में अधिकतम / न्यूनतम मोड़ है या एक काठी बिंदु है। यहां तीन उदाहरण दिए गए हैं, जहां फ़ंक्शन में ढलान
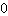
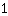
|

है:
इस फ़ंक्शन में ढलान
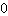
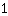
|

और एक अधिकतम मोड़ है। X =
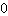
पर ग्राफ चढ़ता है, यानी व्युत्पन्न यहां
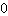
से बड़ा है। X =

पर ग्राफ गिरता है, यानी व्युत्पन्न
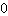
. से कम है। इसका मतलब है कि अधिकतम मोड़ के आसपास, व्युत्पन्न का संकेत मोड़ से पहले और बाद में + है। इसका अर्थ है + से - के लिए व्युत्पन्न परिवर्तन संकेत।
इस फ़ंक्शन में ढलान
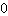
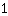
|

है, लेकिन एक न्यूनतम मोड़ है। X =
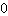
पर ग्राफ गिरता है, यानी यहाँ व्युत्पत्ति कम है
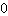
. से अधिक x =

पर ग्राफ बढ़ता है, यानी व्युत्पत्ति
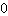
. से बड़ा है। इसका तात्पर्य है कि एक न्यूनतम मोड़ पर, व्युत्पत्ति का संकेत है - मोड़ से पहले और बाद में। इसका मतलब है कि व्युत्पत्ति परिवर्तन के संकेत हैं से - को +।
इस फ़ंक्शन में ढलान
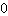
पर
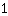
|

भी है, लेकिन कोई मोड़ नहीं है। आप देखें कि ग्राफ x =
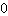
पर और साथ ही x =

पर चढ़ता है। इसका अर्थ है कि यदि व्युत्पत्ति के संकेत नहीं बदलते हैं तो आपके पास कोई मोड़ नहीं है। ऐसा एक बिंदु (जो कोई मोड़ नहीं है लेकिन व्युत्पत्ति
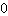
है) को काठी बिंदु कहा जाता है।
संकेत मानदंड के परिवर्तन का उपयोग कैसे करें?
- सबसे पहले अपने फंक्शन की व्युत्पत्ति करें।
- फिर व्युत्पत्ति की जड़ों की गणना करें। केवल वे जड़ें x- निर्देशांक हो सकती हैं नए मोड़।
- फिर आप व्युत्पत्ति जड़ों में एक्स-वैल्यू को व्युत्पत्ति में सम्मिलित करते हैं। अगर व्युत्पत्ति व्युत्पत्ति के चारों ओर संकेत बदलते हैं, आपको एक महत्वपूर्ण मोड़ मिला। नहीं तो नहीं।
संकेतों के परिवर्तन को पर्याप्त मानदंड क्यों कहा जाता है?
व्युत्पत्ति 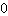 एक मोड़ के लिए आवश्यक है (यानी यह हमेशा एक मोड़ पर स्थिति है)। पर यह आवश्यक नहीं है, क्या मतलब है, सिर्फ इसलिए कि व्युत्पत्ति
एक मोड़ के लिए आवश्यक है (यानी यह हमेशा एक मोड़ पर स्थिति है)। पर यह आवश्यक नहीं है, क्या मतलब है, सिर्फ इसलिए कि व्युत्पत्ति 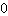 है, एक महत्वपूर्ण मोड़ नहीं है (ऊपर काठी बिंदु के लिए जाँच करें)।
है, एक महत्वपूर्ण मोड़ नहीं है (ऊपर काठी बिंदु के लिए जाँच करें)।
यदि व्युत्पत्ति केवल 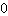 नहीं है, लेकिन यह भी संकेत बदलता है, फिर आपको एक महत्वपूर्ण मोड़ देना होगा। गणित में, हम कहते हैं कि व्युत्पत्ति
नहीं है, लेकिन यह भी संकेत बदलता है, फिर आपको एक महत्वपूर्ण मोड़ देना होगा। गणित में, हम कहते हैं कि व्युत्पत्ति 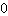 और संकेतों का परिवर्तन पर्याप्त है एक मोड़ होने के लिए।
और संकेतों का परिवर्तन पर्याप्त है एक मोड़ होने के लिए।
क्या मैं एक उदाहरण देख सकता हूं?
बेशक। यह मैथपावर है। बस अपना फ़ंक्शन दर्ज करें और चरण दर चरण गणना के चरण प्राप्त करें।