Tekenwissel criterium



Voer hier de term van uw functie in.
Tip: voer in: als 3*x^2,
als 3/5 en
als (x+1)/(x-2x^4)


Waarvoor heb je het tekenwissel criterium nodig?

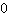
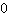
Om te onderscheiden of een functie waarvan de afgeleide 0 is, een maximum, een minimum of een zadelpunt heeft. Drie voorbeelden waarin de functie de helling 0 heeft op punt (1|2):

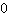
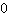
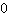
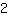
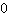
Deze functie heeft een helling van 0 op in (1|2) en een maximum. Bij x = 0 stijgt de grafiek, dat wil zeggen dat de afgeleide hier groter is dan 0. Bij x = 2 daalt deze grafiek, dat wil zeggen, de afgeleide is kleiner dan 0. Dus als een functie een maximum heeft, is het teken van de afgeleide vóór deze maximum + en daarana -. De afgeleide verandert daarom het teken van + in -.



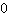
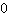
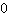
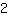
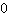
Deze functie heeft een helling van 0 op (1|2), maar een minimum. Bij x = 0 daalt de grafiek, dat wil zeggen dat de afgeleide hier kleiner is dan 0. Bij x = 2 stijgt de grafiek, dat wil zeggen dat de afgeleide groter is dan 0. In dit geval, als een functie een minimum heeft, dan is voor het minimum het teken van de afgeleide - en daarachter een +. De afgeleide verandert daarom van teken van - tot +.



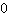
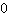
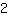
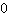
Deze functie heeft tevens een helling 0 op (1|2), maar geen maximum of minimum. Je kunt zien dat de grafiek stijgt bij x = 0 en bij x = 2. Als de afleiding niet van teken verandert, is er blijkbaar geen maximum. Zo'n punt (dat geen maximum of minimum is maar toch een afgeleide van 0 heeft) wordt zadelpunt genoemd.

Hoe gebruik je het tekenwissel criterium ?

  • Eerst bepaal je de afgeleide functie.
  • Vervolgens bepaal je de nulpunten van de afgeleide. Alleen deze nulpunten kunnen x-coördinaten zijn van maxima of minima
  • Ten slotte plaatst u waarden in de buurt van de nulpunten in de afgeleide. Als de afgeleide in de buurt van het nulpunt van teken wisselt, dan heb je een maximum of minimum gevonden. Anders niet.

    • Waarom is het tekenwissel criterium een voldoende criterium?

    Dat de afgeleide gelijk is aan 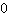0 is nodig voor een extreme waarde (wat betekent: noodzakelijk bij een extreme waarde). Ja, maar niet voldoende voor een maximum of minimum, wat betekent dat alleen omdat de afgeleide 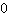0 is, je geen maximum of minimum hoeft te hebben (zie hierboven bij het zadelpunt).
    Als niet alleen de afgeleide 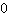0 is, maar ook van teken verandert, dan moet je een maximum of minimum hebben. In de wiskunde zeggen ze dat afgeleide 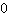0 en tekenwissel voldoende is voor een maximum of minimum.

    Kan ik een voorbeeld bekijken?

    Natuurlijk. Dit is Mathepower. Voer gewoon je functie in en laat de extreme waarden stap voor stap berekenen.