Per i triangoli valgono le seguenti proprietà:
Teorema del seno:
a / b = sin alfa / sin beta
Teorema del coseno:
a² = b² + c² - 2bc cos alpha
Triangoli
Cos'è un triangolo?
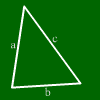
Qui possiamo osservare un triangolo.
Un triangolo ha tre lati e tre angoli.
Ad ogni angolo si definisce angolo interno l'angolo delimitato da due lati adiacenti.
La somma degli angoli interni è sempre di 180 gradi in un triangolo.
Con quali dati un triangolo è definito univocamente?
Si definisce univocamente un triangolo tramite la lunghezza dei suoi tre lati, tramite due angoli e la lunghezza di un lato oppure tramite due lati e l'angolo tra essi compreso.Ci sono anche altri casi in cui un triangolo è definito da tre parametri ma in modo non univoco. Ad esempio, dati due lati e l'altezza su uno di essi, ci sono due modi per costruire il triangolo. Tuttavia, le possibilità sono limitate massimo a due per determinare un triangolo tramite tre parametri.
Cos'è l'altezza di un triangolo?
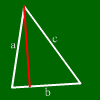
L'altezza è la distanza che congiunge perpendicolarmente un vertice al lato opposto.
Che formule descrivono le proprietà di un triangolo?
L'area di superficie si calcola con base*altezza/2 per ogni lato e la sua rispettiva altezza.Lati e angoli possono essere calcolati usando le leggi del seno e coseno. Il teorema del seno mette in relazione due lati e gli angoli ad essi opposti:
a/sin alfa = b/sin beta (teorema del seno).
Il teorema del coseno lega due lati e l'angolo da essi delimitato con il terzo lato:
a^2 = b^2 + c^2 - 2*b*c*cos gamma (teorema del coseno).
Che segmenti particolari sono definiti in un triangolo?
Segmenti particolari sono gli assi, le bisettrici degli angoli, le mediane e le altezze.Quali particolari tipi di triangoli sono importanti?
Particolari tipologie sono il triangolo isoscele, il triangolo equilatero e il triangolo rettangolo. Nei restanti casi il triangolo viene detto scaleno.Per maggiori informazioni sposta il mouse su una delle parole qui sotto e la componente corrispondente del triangolo verrà evidenziata.
Lato a,
Lato b,
Lato c
Angolo alfa, Angolo beta, Angolo gamma
Altezza su a, Altezza su b, Altezza su c
Mediana su a, Mediana su b, Mediana su c
Bisettrice di alfa, Bisettrice di beta, Bisettrice di gamma
Area di superficie