O que seria um esboço de curva?
Esboço de curva é um cálculo para encontrar pontos característicos de uma função, por exemplo, raízes, eixo-y intersepto, pontos extremos máximos e mínimos e pontos de inflexão.
Como acho esses pontos?
Calculando as derivadas. Defina que a derivada da função seja zero: As raízes serão a solução da equação
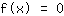
. Pontos extremos podem ser a raíz da derivada, ou seja, você tem que resolver a equação
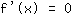
para encontrar o ponto extremo máximo/mínimo. (para saber se há ou não pontos extemos na raíz da derivada, basta usar o critério de troca de sinais. Já no ponto de inflexão, a segunda derivada deve ser
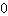
, então resolva a equação para encontrar esse ponto
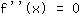
.
Por que o esboço de curva não é tão usado hoje em dia?
É simples: Você só precisa aprender o mesmo cálculo de sempre sem ter que pensar muito a respeito. Diferente dos exercícios de hoje em dia em que pensar mais se torna mais importante.
Posso ver um exemplo?
Claro! Vamos lá
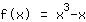
Mathepower funciona com essa função:
Aqui está o gráfico da sua função.
|
|
- Raízes á -1; 0; 1
- intercepção do eixo-y á (0|0)
- Mais alto e mais baixo ponto extremo á (-0.577|0.385); (0.577|-0.385)
- Pontos de inflexão á (0|0)
Isto é o que a Mathepower calculou:
Raízes:
Procurando a raíz 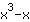
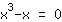 | | | Fator 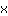 . . |
 | | | 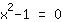 | | | O produto é igual a 0. Então o fator 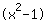 deve ser zero... deve ser zero... |
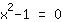 | | | +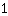 |
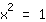 | | | Extraia a raíz quadrada de ambos os lados |
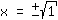 | | | 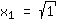 | | | Extraia a raíz 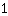 |
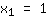 | | | 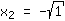 | | | Extraia a raíz 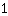 |
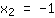 | | | 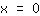 | | | ...ou o fator 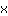 deve ser zero... deve ser zero... |
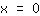 | | |
Então, as raízes são: {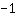 ; ;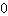 ; ;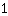 } }
Simetria
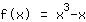 é um ponto simétrico à origem. é um ponto simétrico à origem.
Calcule a intercepção do eixo-y inserindo 0.
Insira 0 na função 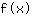 : :
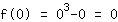
Então, a intercepção do eixo-y está em (0|0)
Derive a função 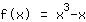
| Derivada da função 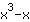 : : | ( Derivada  ) ) | + | ( Derivada 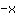 ) ) | 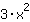 | + | 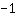 |
Então, a derivada de 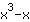 é é 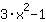 . . |
| |
|
Então a primeira derivada é: 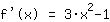
Segunda derivada, ou seja, derivada de 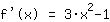 : :
| Derivada da função 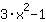 : : | ( Derivada 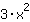 ) ) | + | ( Derivada 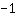 ) ) | 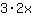 | + | 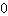 |
Então, a derivada de 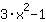 é é 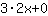 . . |
| |
|
Simplifique a derivada:
Então a segunda derivada é 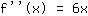
Terceira derivada, ou seja, derivada de 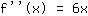 : :
A derivada de 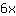 é é 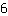
Então a terecira derivada é 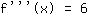
Procurando por pontos extremos.
Temos que encontrar a raíz da primeira derivada.
Procurando a raíz 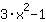
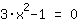 | | | +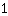 |
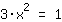 | | | : 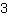 |
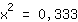 | | | Extraia a raíz quadrada de ambos os lados |
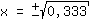 | | | 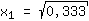 | | | Extraia a raíz  |
 | | | 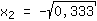 | | | Extraia a raíz  |
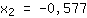 | | |
Os pontos extremospodem estar em {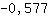 ; ;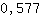 } }
Insira a raíz da primeira derivada na segunda derivada:
Insira -0.577 na função 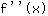 : :
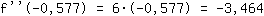
-3.464 é menor que 0. Então existe um máximo 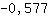 . .
Insira -0.577 na função 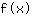 : :
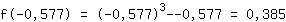
Ponto extremo máximo (-0.577|0.385)
Insira 0.577 na função 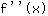 : :

3.464 é maior que 0. Então existe um mínimo 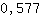 . .
Insira 0.577 na função 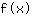 : :
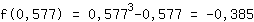
Ponto extremo mínimo (0.577|-0.385)
Procurando o ponto de infexão.
É preciso encontrar a raíz da segunda derivada.
Procurando a raíz 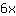
O ponto de inflexão podem estar em {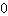 } }
Insira a raíz da segunda derivada na terceira derivada:
x , então é fornecida por inserção 6
6 é maior que 0. Então existe um ponto de inflexão 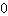 . .
Insira 0 na função 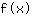 : :
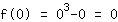
Ponto de inflexão (0|0)
|