¿Cómo resolver ecuaciones lineales?
Un ejemplo:
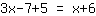
Primero, simplifica en ambos lados. En el lado izquierdo puedes sumar

y
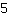
. Entonces obtienes la ecuación:
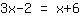
El paso siguiente es,de reorganizar la ecuación, quiere decir, despejar x al lado izquierdo y poner los números al lado derecho. Ya que no queremos tener el x en el lado derecho,tenemos que restar x en ambos lados.
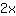
queda en el lado izquierdo.
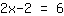
Ahora, tenemos que poner el número
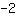
al otro lado. Entonces añadimos
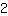
en ambos lados. Por tener
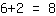
y obtenemos
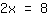
El sigiente paso es dividir ambos lados por el número delante de x:
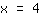
La ecuación está resuelta;
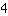
es su solución.
De esta manera puedes proceder siempre: Primero, simplifica ambos lados de la ecuación tanto como sea posible. Después, simplifica con transformaciones equivalentes. Resta apropiadamente un número en ambos lados. Al final deberías tener varios variables en un lado y un número en el otro lado. Divides por el número delante de la variable y la ecuación está resuelta.
¿Cómo presenta Mathepower soluciones?
Cuando introduces una ecuación, recibes lo siguiente:
| Tu problema matemático: | | Explicación paso a paso: |
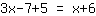 | | | multiplica  [multiplica x] y [y] [multiplica x] y [y] 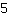 |
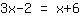 | | | 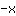 |
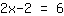 | | | +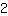 |
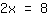 | | | : 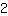 |
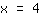 | | |
Conjunto de soluciones: { } } |
¿Y si quiero resolver otra ecuación?
Estas en mathepower.com. Introduce tu ecuación arriba y se resuelve de la misma manera. Inmediatamente y gratis (mathepower esta financiado por publicidad).
¿Qué casos especiales hay que considerar resolviendo ecuaciones?
Los casos especiales más importantes son ecuaciones que tienen un número infinito de soluciones o que no tienen solución.
Primero, un ejemplo de una ecuación con un número infinito de soluciones:
| Tu problema matemático: | | Explicación paso a paso: |
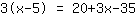 | | | Aplica la propiedad distributiva 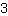 y y  . . |
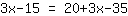 | | | multiplica 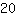 [multiplica x] y [y] [multiplica x] y [y] 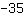 |
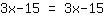 | | |  |
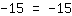 | | | | La ecuación es válida universalmente. |
|
Conjunto de soluciones: R |
Se ve que acabamos con los mismos números en ambos lados. Evidentemente se trata de una confirmación verdadera para cada valor de x (ya no hay ningun x en esta ecuación). De esta manera , vemos que la ecuación puede tener un número infinito de soluciones.
¿Qué significa una ecuación tiene un número infinito de soluciones? Puedes probar lo siguiente: Inserta cualquier valor para x (p.ej.
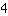
ambos lados van a tener el mismo resultado. Esto funciona con cualquier valor de x. La razón es, que los términos en ambos lados son equivalentes es decir, términos que tienen la misma solución con cualquier valor de x.
El otro caso especial es una ecuación que no tiene solución:
| Tu problema matemático: | | Explicación paso a paso: |
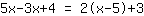 | | | multiplica 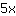 [multiplica x] y [y] [multiplica x] y [y]  |
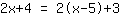 | | | Aplica la propiedad distributiva 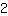 y y  . . |
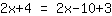 | | |
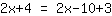 | | | multiplica 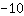 [multiplica x] y [y] [multiplica x] y [y] 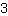 |
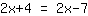 | | | 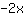 |
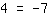 | | | | La ecuación no tiene solución. |
|
Conjunto de soluciones: {} |
Aquí vemos que no hay ningun x en la ecuación después de transformarla así que la ecuación es evidentemente falsa. Esto se debe al hecho de que la ecuación original no tiene solución.