Wie löst man lineare Gleichungen?
Erst einmal ein Beispiel:
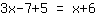
Zunächst fasst man die beiden Seiten zusammen. Auf der linken Seite kann man
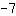
und
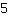
addieren. Dann hat man die
Gleichung:

Als nächstes stellt man die Gleichung um, und zwar so, dass x nur noch links steht und rechts nur Zahlen. Das x stört rechts, also zieht man auf beiden Seiten ein x ab. Links bleiben dann noch
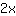
übrig.
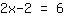
Jetzt bringt man noch die Zahl
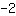
auf die andere Seite, indem man auf beiden Seiten
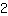
addiert. Wegen
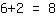
hat man dann
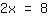
Jetzt noch auf beiden Seiten durch die Zahl vor dem x teilen:
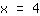
Die Gleichung ist gelöst,
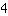
ist also eine Lösung der Gleichung.
Auf die gleiche Weise kann man immer vorgehen: Erst die beiden Seiten so weit wie möglich zusammenfassen und vereinfachen. Dann weiter vereinfachen durch Äquivalenzumformungen: Geschickt etwas abziehen, was auf beiden Seiten steht. Schliesslich sollte auf der einen Seite nur noch ein Vielfaches der Variablen stehen und auf der anderen eine Zahl. Man teilt durch die Zahl vor der Variablen und hat die Gleichung gelöst.
Wie stellt Mathepower das ganze dar?
Wenn du deine Gleichung einfach eingibst, erhältst du:
| Deine Aufgabe: | | Erklärung der Zwischenschritte: |
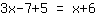 | | | addiere 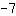 und und 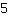 |
 | | | 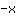 |
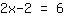 | | | +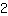 |
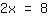 | | | : 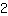 |
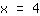 | | |
Lösungsmenge: {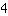 } } |
Und wenn ich eine andere Gleichung gelöst haben will?
Das hier ist mathepower.com . Gib doch einfach deine Gleichung oben ein und sie wird nach dem gleichen Verfahren gelöst. Sofort und kostenlos (Mathepower finanziert sich durch Werbung).
Welche Sonderfälle gibt es beim Gleichung lösen?
Die wichtigsten Sonderfälle sind, wenn die Gleichung allgemeingültig ist oder wenn sie gar keine Lösungen hat.
Erst einmal ein Beispiel für eine allgemeingültige Gleichung:
| Deine Aufgabe: | | Erklärung der Zwischenschritte: |
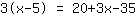 | | | Multipliziere 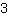 und und 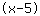 aus. aus. |
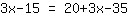 | | | addiere 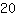 und und 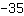 |
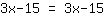 | | | 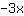 |
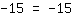 | | | | Die Gleichung ist allgemeingültig. |
|
Lösungsmenge: R |
Man sieht, dass hinterher auf beiden Seiten die gleiche Zahl steht, also eine offensichtlich wahre Aussage, egal welchen Wert x hat (es ist ja auch gar kein x mehr drin). Auf diese Weise sehen wir, dass eine Gleichung allgemeingültig ist.
Was heißt jetzt also, dass eine Gleichung allgemeingültig ist? Man kann ausprobieren: Setzt man in die ursprüngliche für x irgendeine Zahl ein (z.B.
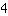
, so kommt auf beiden Seiten das Gleiche raus. Das wird mit jedem Wert für x funktionieren. Der Grund dafür ist, dass auf beiden Seiten der Gleichung äquivalente
Terme stehen, soll heißen, Terme, die für jedes Zahleneinsetzen das gleiche Ergebnis liefern.
Der andere Sonderfall ist eine Gleichung, die überhaupt keine Lösungen hat:
| Deine Aufgabe: | | Erklärung der Zwischenschritte: |
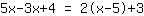 | | | addiere 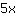 und und 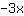 |
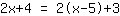 | | | Multipliziere 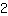 und und 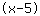 aus. aus. |
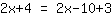 | | |
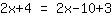 | | | addiere 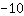 und und 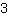 |
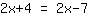 | | | 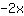 |
 | | | | Die Gleichung hat keine Lösungen. |
|
Lösungsmenge: {} |
Wie wir hier sehen, entsteht durch Umformen eine Gleichung, in der gar kein x mehr vorkommt und die offensichtlich falsch ist. Dies liegt daran, dass die ursprüngliche Gleichung schon keine Lösungen hatte.