Scheitelpunktform

<

Scheitelpunktform

Gib hier die Funktion ein, die auf Scheitelpunktform gebracht werden soll.

Eingabetipp: Gib als 3*x^2 ein.






Was ist die Scheitelpunktform?

Die Scheitelpunktform ist eine spezielle Form der quadratischen Funktion. An der Scheitelpunktform kann man besonders schnell sehen, wo der höchste bzw. tiefste Punkt (der Scheitelpunkt) einer Parabel ist: Die Zahl in der Klammer gibt (Vorsicht: bis auf das Vorzeichen!) die x-Koordinate des Scheitelpunktes an, die Zahl ganz hinten die y-Koordinate.

Wie bringt mane eine Funktion auf Scheitelpunktform?

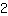
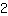
Dazu muss man die sogenannte quadratische Ergänzung durchführen: Man nimmt die Zahl vor dem x geteilt durch 2 und rechnet das Ergebnis dann wiederum hoch 2. Hier ein Beispiel:


Mathepower rechnet mit dieser Funktion:

Ergebnis: Scheitelpunktform 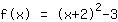f(x)=1*(x+2)^2+-3
und Scheitelpunkt (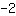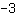-2|-3)

Hier siehst du den Graphen deiner Funktion.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Scheitelpunkt bei (-2|-3)
Mathepower hat wie folgt gerechnet:
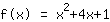f(x)=1*x^2+4*x+1
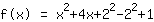f(x)=x^2+4*x+(2)^2+-1*(2)^2+1(quadratisch ergänzen)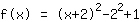
f(x)=(x+2)^2+-1*(2)^2+1(binomische Formel bauen)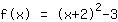
f(x)=(x+2)^2+-3(vereinfachen)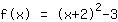
f(x)=1*(x+2)^2+-3(ausmultiplizieren)

Wie man sieht, ist die x-Koordinate des Scheitelpunkts genau das Negative von der Zahl, die in der Klammer steht. Außerdem sieht man an der Rechnung, dass man eigentlich die binomische Formel "rückwärts" anwenden muss: Man muss sich aus dem Funktionsterm eine binomische Formel bauen. Das geht aber nicht immer, sondern nur, wenn die passende Zahl (die quadratische Ergänzung) dasteht. Also ergänzt man einfach die quadratische Ergänzung und zieht sie auch gleich wieder ab.

Und wenn vor dem 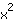x^2 noch eine Zahl steht?

Dann muss man diese zunächst ausklammern. Beispiel:


Mathepower rechnet mit dieser Funktion: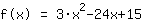
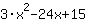=3*x^2+-1*24*x+15

Ergebnis: Scheitelpunktform 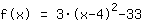f(x)=3*(x+-4)^2+-33
und Scheitelpunkt (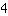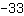4|-33)

Hier siehst du den Graphen deiner Funktion.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Scheitelpunkt bei (4|-33)
Mathepower hat wie folgt gerechnet:
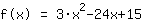f(x)=3*x^2+-24*x+15
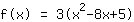f(x)=3*(x^2+-8*x+5)(zuerst ausklammern)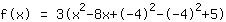
f(x)=3*(x^2+-8*x+(-4)^2+-1*(-4)^2+5)(quadratisch ergänzen)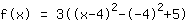
f(x)=3*((x+-4)^2+-1*(-4)^2+5)(binomische Formel bauen)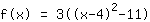
f(x)=3*((x+-4)^2+-11)(vereinfachen)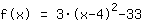
f(x)=3*(x+-4)^2+-33(ausmultiplizieren)

Wichtig: Erst ausklammern, dann erst quadratisch ergänzen! Andernfalls könnte man die binomische Formel nicht rückwärts anwenden. (Leider denken viele Schüler über solche Feinheiten nicht nach und wenden einfach trotzdem die binomische Formel rückwärts an, auch wenn es nicht geht... Schade, dass Terme nicht "AUA" schreien können, sondern nur Mathelehrer beim Anblick einer solchen Rechnung.)

Und wenn vor dem 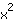x^2 ein Minus steht?

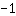
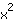
Dann muss man -1 ausklammern. Übrigens ist immer, wenn vor dem x^2 ein negativer Faktor steht, die Parabel nach unten geöffnet. Beispiel:


Mathepower rechnet mit dieser Funktion: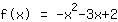
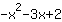=-1*x^2+-1*3*x+2

Ergebnis: Scheitelpunktform 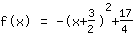f(x)=-1*(x+3/2)^2+17/4
und Scheitelpunkt (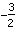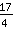-3/2|17/4)

Hier siehst du den Graphen deiner Funktion.
Dein Browser unterstützt den HTML-Canvas-Tag nicht. Hol dir einen neuen. :P
  • Scheitelpunkt bei (-1.5|4.25)
Mathepower hat wie folgt gerechnet:
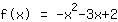f(x)=-1*x^2+-3*x+2
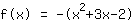f(x)=-1*(x^2+3*x+-2)(zuerst ausklammern)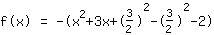
f(x)=-1*(x^2+3*x+(3/2)^2+-1*(3/2)^2+-2)(quadratisch ergänzen)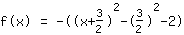
f(x)=-1*((x+3/2)^2+-1*(3/2)^2+-2)(binomische Formel bauen)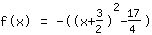
f(x)=-1*((x+3/2)^2+1*-17/4)(vereinfachen)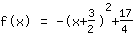
f(x)=-1*(x+3/2)^2+17/4(ausmultiplizieren)

Und wie lautet die Scheitelpunktform allgemein?

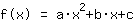
Kein Problem, das kann Mathepower ausrechnen. Geben wir doch einfach die Funktion f_f(x)=ax^2+bx+c ein.


Mathepower rechnet mit dieser Funktion:

Ergebnis: Scheitelpunktform 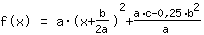f(x)=1*a*(x+b/(2*a))^2+(1*a*c+-0.25*b^2)/a
und Scheitelpunkt (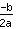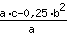(-1*b)/(2*a)|(1*a*c+-0.25*b^2)/a)

Mathepower hat wie folgt gerechnet:
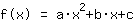f(x)=1*a*x^2+1*b*x+1*c
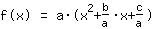f(x)=1*a*(x^2+b/a*x+c/a)(zuerst ausklammern)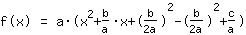
f(x)=1*a*(x^2+b/a*x+(b/(2*a))^2+-1*(b/(2*a))^2+c/a)(quadratisch ergänzen)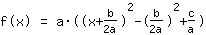
f(x)=1*a*((x+b/(2*a))^2+-1*(b/(2*a))^2+c/a)(binomische Formel bauen)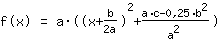
f(x)=1*a*((x+b/(2*a))^2+1*(1*a*c+-0.25*b^2)/a^2)(vereinfachen)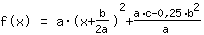
f(x)=1*a*(x+b/(2*a))^2+(1*a*c+-0.25*b^2)/a(ausmultiplizieren)

Kann ich noch mehr Beispiele sehen?

Klar. Das hier ist Mathepower.com . Gib einfach dein Beispiel oben ein und es wird ausgerechnet.