Worum geht es?
Wenn man im dreidimensionalen Raum einen Punkt und eine Ebene hat, dann kann man ausrechnen, wie weit der Punkt von der Ebene
entfernt ist. Damit ist gemeint, wie lang der kürzeste Abstand des Punktes von einem Punkt der Ebene ist.
Und wie berechnet man diesen Abstand?
Ein gutes Verfahren ist es, vom Punkt aus einen Weg zu gehen, der senkrecht auf der Ebene steht. Dazu ist es sinnvoll, den
Normalenvektor der Ebene zu berechnen. Wenn man diesen auch noch normiert, sprich, auf Länge 1 bringt, ist dies für den weiteren
Rechenweg von Vorteil. Baut man nämlich eine Gerade, die den Punkt als Ortsvektor und den normierten Normalenvektor als
Richtungsvektor hat, dann kann man den Abstand leicht berechnen.
Das klingt kompliziert. Kann ich mal ein Beispiel sehen?
Klar.
Aufgabe: Abstand des Punktes
( 3 | 4 | 1 ) von der Ebene
soll berechnet werden
Schritt 1: Normierten Normalenvektor der Ebene bestimmen.
Ein normierter Normalenvektor von
soll bestimmt werden.
| Ein solcher Vektor erfüllt die Gleichungen | | ⋅ | | =0 |
Also sind x,y,z Lösungen der beiden Gleichungen
| 2x | +4y | +3z | = | 0 |
| x | +4y | +2z | = | 0 |
So formt man das Gleichungssystem um:
| 2x | +4y | +3z | = | 0 | | x | +4y | +2z | = | 0 |
| |
| 2x | +4y | +3z | = | 0 | | | 2y | +0,5z | = | 0 |
| ( das -0,5-fache der ersten Zeile wurde zur zweiten Zeile addiert )
|
| x | +2y | +1,5z | = | 0 | | | 2y | +0,5z | = | 0 |
| ( die erste Zeile wurde durch 2 geteilt ) |
| x | +2y | +1,5z | = | 0 | | | y | +0,25z | = | 0 |
| ( die zweite Zeile wurde durch 2 geteilt ) |
| zweite Zeile: | y+0,25z = 0 |
| z frei wählbar. |
| Nach y freistellen: | y = -0,25z |
| erste Zeile: | |
| Schon berechnete Variablen einsetzen: | | x | +2⋅(-0,25z ) | +1,5⋅1z | = | 0 |
|
| Nach x freistellen: | x = -1z |
Setzt man z = 1, so erhält man den Normalenvektor
| Betrag von | | ist gleich | 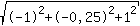 | =1,44 |
Vektor normieren, also mit 1/Betrag malnehmen:
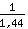 ⋅ ⋅ | | = | |
Schritt 2: Gerade
| g: x= | ( | 3 | ) | +r | ( | -0,7 | ) |
| 4 | -0,17 |
| 1 | 0,7 |
mit
schneiden
Aufgabe: Schnittpunkte finden von
| g: x= | ( | 3 | ) | +r | ( | -0,7 | ) | | 4 | -0,17 | | 1 | 0,7 |
| und | |
Vektorgleichung (bedenke, Parameter umzubenennen...):| ( | 3 | ) | +r | ( | -0,7 | ) | = | ( | 2 | ) | +s | ( | 2 | ) | +t | ( | 1 | ) | | 4 | -0,17 | 3 | 4 | 4 | | 1 | 0,7 | 5 | 3 | 2 |
Das liefert das folgende Gleichungssystem:| 3 | -0,7r | = | 2 | +2s | +t | | 4 | -0,17r | = | 3 | +4s | +4t | | 1 | +0,7r | = | 5 | +3s | +2t |
So formt man das Gleichungssystem um:
| -0,7r | -2s | -1t | = | -1 | | -0,17r | -4s | -4t | = | -1 | | 0,7r | -3s | -2t | = | 4 |
| ( Variablen wurden nach links gebracht, Zahlen nach rechts. ) | | -0,7r | -2s | -1t | = | -1 | | -0,17r | -4s | -4t | = | -1 | | | -19s | -18t | = | 0 |
| ( das 4-fache der zweiten Zeile wurde zur dritten Zeile addiert )
| | -0,7r | -2s | -1t | = | -1 | | | -3,5s | -3,75t | = | -0,75 | | | -19s | -18t | = | 0 |
| ( das -0,25-fache der ersten Zeile wurde zur zweiten Zeile addiert )
| | r | +2,87s | +1,44t | = | 1,44 | | | -3,5s | -3,75t | = | -0,75 | | | -19s | -18t | = | 0 |
| ( die erste Zeile wurde durch -0,7 geteilt ) | | r | +2,87s | +1,44t | = | 1,44 | | | -3,5s | -3,75t | = | -0,75 | | | | 2,36t | = | 4,07 |
| ( das -5,43-fache der zweiten Zeile wurde zur dritten Zeile addiert )
| | r | +2,87s | +1,44t | = | 1,44 | | | s | +1,07t | = | 0,21 | | | | 2,36t | = | 4,07 |
| ( die zweite Zeile wurde durch -3,5 geteilt ) | | r | +2,87s | +1,44t | = | 1,44 | | | s | +1,07t | = | 0,21 | | | | t | = | 1,73 |
| ( die dritte Zeile wurde durch 2,36 geteilt ) |
| zweite Zeile: | | | Schon berechnete Variablen einsetzen: | | | Nach s freistellen: | s = -1,64 |
| erste Zeile: | | | Schon berechnete Variablen einsetzen: | | r | +2,87⋅(-1,64) | +1,44⋅1,73 | = | 1,44 |
| | Nach r freistellen: | r = 3,66 |
Werte in Ebene einsetzen:
|
Also muss man vom Punkt aus den normierten Normalenvektor 3,66-mal gehen, um auf der Ebene zu sein.
Also beträgt der Abstand 3,66.
Kann ich noch ein Beispiel sehen?
Klar, gib oben einfach deine eigene Aufgabe ein. Sie wird sofort kostenlos ausgerechnet.