¿Qué es una tangente?
Una tangente es una recta que toca algo sin cruzarlo. Por ejemplo, si pones una pelota en el suelo, la pelota sólo toca el suelo pero no lo cruza. Entonces el suelo sería la tangente a la pelota.
Aquí tienes dos ejemplos:
La recta verde no es una tangente porque la recta cruza la gráfica. La recta roja es una tangente porque sólo toca la gráfica en un punto sin cruzarla.
Un caso particular: Una tangente en un punto de inflexión cruza la gráfica de la función. De todas formas, la recta roja es evidentemente la tangente en el punto (0|0) que tiene la misma pendiente como la gráfica.
También ten en cuenta: Una recta que es tangente en en punto puede cruzar la gráfica en otro punto.
¿Por qué determinamos las tangentes a las gráficas de funciones?
Si determinas una tangente a una gráfica en un punto, puedes decir que la gráfica tiene la misma pendiente como la tangente. Entonces se usa tangentes para determinar la pendiente de una gráfica.
¿Cómo se calcula una tangente?
Si quieres determinar la tangente en el punto x tienes que hacer tres cosas:
- Inserta x en la función así calculas el punto en el que toca la tangente
- Inserta x en la derivada así determinas la pendiente m de la tangente.
- Inserta m y el punto en
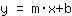así determinas b
¿Puedo ver más ejemplos?
Por supuesto. Sólo inserta una función y un punto en nuestra calculadora gratuita arriba. Mathepower determina la tangente paso a paso.