حاسبة فيثاغورس

بالنسبة للمثلثات القائمة ، يتم تطبيق الصيغ التالية:
t_2
a² + b² = c² (نظرية فيثاغورس)
a² = c * p و b² = c * q (نظرية إقليدس )
h² = p * q (نظرية ارتفاع إقليدس)
sin alpha = a/c

المثلثات القائمة

ما هو المثلث قائم الزاوية؟

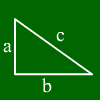
المثلث قائم الزاوية هو (كما يقول الاسم) مثلث يحتوي على زاوية قائمة (أي مستطيل 90 درجة). تجعل هذه الخاصية الحسابات سهلة للغاية.
يسمى الضلع المقابل للزاوية القائمة الوتر ، وتسمى الأضلاع الأخرى الأضلاع القائمة أو الساقين.
في المثال الموجود على اليسار تكون الزاوية القائمة مقابلة لـ c. لذلك ، c هي الوتر و a و b هما الساقين.

ما هي الصيغ التي تطبق على المثلث قائمة الزاوية؟

في المثلث القائم الزاوية ، تحمل نظرية فيثاغورس: a & sup2 + b & sup2 = c & sup2. هذا يعني أن c تساوي الجذر التربيعي لـ (a & sup2 + b & sup2) أو b تساوي الجذر التربيعي لـ (c & sup2 - a & sup2).
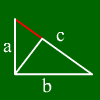
علاوة على ذلك ، بالنسبة لأجزاء الوتر (تسمى p و q ، p كونها أقل من a و q تحت b) فإن تلك الصيغ تحمل:
a² = c * p و b² = c * q (نظرية إقليدس )
الصيغة الثالثة هي قاعدة الارتفاع التي تجعل العبارة التالية حول الارتفاع في c: h² = p * q.
كما يتم حساب مساحة المثلث القائم بسهولة لأنها تساوي ببساطة (ساق * ساق أخرى) / 2.

لمزيد من المعلومات ، ما عليك سوى تحريك الماوس فوق إحدى الكلمات أدناه وسيتم تمييز الجزء المقابل من المثلث.

الساق a الساق b وتر المثلث القائم c
جزء الوتر p جزء الوتر q المساحة الارتفاع على c

نظرية فيثاغورس

كيف تثبت نظرية فيثاغورس؟

يظهر أحد الاحتمالات من خلال الرسوم المتحركة فلاش لدينا:



حاسبة فيثاغورس المجانية من Mathepower . على سبيل المثال يمكنك الحساب باستخدام الصيغة a² + b² = c² أو صيغ أخرى.