Berechnungen am Trapez - Flächeninhalt und Umfang berechnen
 
Klassen 1-4
Schriftliche Addition
Schriftliche Subtraktion
Schriftliche Multiplikation
Schriftliche Division
Zahlen in Worten

Klasse 5
Größen umrechnen
Rechnen mit Einheiten
Zahlensysteme
Quadrat
Rechteck
Römische Zahlen
Klammeraufgaben

Klasse 6
Primfaktorzerlegung
Teilbarkeitstest
Teilermenge
ggT
kgV
Brüche kürzen
Brüche addieren
Brüche subtrahieren
Brüche malnehmen
Brüche teilen
Längere Bruchaufgaben
Bruch, Kommazahl
Rechteck
Quader
Würfel

Klasse 7
Prozentrechnung
Rationale Zahlen
Terme vereinfachen
Proportionalitäten
Antiproportionalitäten
Dreieck
Zinsrechnung
Dreisatz
Antiproportionaler Dreisatz

Klasse 8
Terme vereinfachen
Gleichungen lösen
Ungleichungen
Binomische Formeln
Bruchterme
Gleichung freistellen
Quader
Parallelogramm
Raute
Trapez
Kreis

Klasse 9
Quadrieren
Wurzel ziehen
Rechtwinkliges Dreieck
Satz des Pythagoras
Quadratische Gleichungen
Terme
Gleichungssysteme
Wurzelterme
Wurzelgleichungen
Bruchgleichungen
Gleichung auflösen

Klasse 10
Sinus, Cosinus, Tangens
Potenzrechnung
Dreieck
Kreisbogen
Kegel
Kegelstumpf
Prisma
Pyramide
Pyramidenstumpf
Zylinder

Gleichungen
Bruchgleichungen
Gleichungen
Gleichungssysteme
Lineare Gleichungen
Quadratische Gleichungen
Ungleichungen
Wurzelgleichungen

Geometrie
Dreieck
Rechtwinkliges Dreieck
Kegel
Kegelstumpf
Kreis
Kreisbogen
Parallelogramm
Prisma
Pyramide
Pyramidenstumpf
Quader
Quadrat
Raute
Rechteck
Satz des Pythagoras
Sinus, Cosinus, Tangens
Trapez
Würfel
Zylinder

Sonstiges
Mathe-Suchmaschine
Gleichung erkennen
Hilfe
Forum
Mathe-Shop
Fehler gefunden
Links
Werbung
Impressum
Link zu Mathepower

als Startseite
zu den Favoriten
Seite empfehlen
 

 

 

 

 

 
 

Trapez berechnen


Vier beliebige Felder sind auszufüllen. Rest wird berechnet
Es wird davon ausgegangen, daß a und c parallel sind.
Dieses Skript ist durchaus unvollständig, da vier Angaben bei einem Trapez nur selten eines eindeutig definieren.

a: b: c: d:
Alpha: Beta: Gamma: Delta:
Höhe:
Diagonale e: Diagonale f:
Flächeninhalt:


Ein Trapez.
Für Trapeze gilt:
Alpha + Delta = Beta + Gamma = 180 Grad
Flächeninhalt = (a+c)/2 * Höhe
Für ausführliche Infos zum Thema klick hier.

Trapeze

Was ist ein Trapez?
Ein Trapez ist ein Viereck mit zwei parallelen Seiten. Da von dem Viereck also nicht sehr viel gefordert wird, ist es meist recht schwierig, Berechnungen an ihm durchzuführen. Immerhin hat man eine einfache Formel für den Flächeninhalt, F=(a+c)/2*h, wobei a und c die parallelen Seiten sind und h die Höhe, also ihr Abstand. Außerdem weiß man, daß zwei benachbarte Winkel, die jeweils an verschiedenen der parallelen Seiten liegen, eine Winkelsumme von 180 Grad haben.

Wie kann man sich die Trapezformeln anschaulich vorstellen?
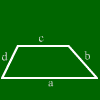Die meisten Trapezformeln stellt man sich anschaulich so vor, daß man die Ecken des Trapezes geschickt so abschneidet und umklebt, daß man hinterher ein Rechteck erhält. Ein Trapez. Seite a, Seite b, Seite c, Seite d
Winkel Alpha, Winkel Beta, Winkel Gamma, Winkel Delta
Diagonale e, Diagonale f
Flächeninhalt
Höhe