Wozu braucht man Brüche?
Erst einmal ein Beispiel: Stellt euch vor, man will zu viert einen Kuchen essen. Wie viel Kuchen bekommt dann jeder? Was man rechnen muss, ist
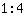
, so viel ist klar. Aber was kommt da raus? In der Grundschule hätte man jetzt gesagt,
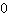
Rest
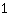
. Das bringt uns aber nicht viel weiter. Stattdessen schaffen wir uns eine neue Zahl namens
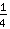
(gesprochen: ein Viertel). Wenn ihr euch vorstellen wollt, wie viel das ist, malt euch doch einmal einen Kuchen auf und teilt ihn ihn vier gleich große Stücke.
Und was ist so ein Bruch?
Was wir gerade mit dem Kuchen gemacht haben, kann man mit allen Zahlen machen: Man stelle sich vor, man habe zwei natürliche Zahlen und wolle die durcheinander teilen, aber es geht nicht auf. Was macht man also? Man stellt sich einfach vor, man könnte es, und denkt sich eine Zahl aus, die das Ergebnis dieser Division ist. Also bedeutet der Bruch
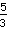
nichts anderes als ' das Ergebnis der Rechnung
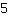
durch
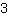
'. Die Zahl oben im Bruch nennt man Zähler, die unten Nenner. Beim Bruch
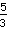
ist der Zähler also
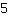
und der Nenner
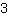
.
Und wie rechnet man mit solchen Brüchen?
Erst mal überlege man sich: Es gibt verschieden aussehende Brüche, die die gleiche Zahl meinen. Zum Beispiel ist
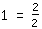
oder
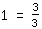
, weil
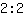
und
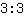
beide gerade
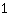
ergeben.
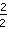
und
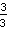
sehen also verschieden aus, stellen aber beide die gleiche Zahl dar. Einen Bruch in einen anderen umzuwandeln, der die gleiche Zahl darstellt, nennt man
erweitern oder kürzen.
Will man Brüche addieren oder abziehen, so muss man sie vorher gleichnamig machen, das heißt, sich einen gemeinsamen Nenner für beide Brüche überlegen. Das schafft man, in dem man sich das
kleinste gemeinsame Vielfache der beiden Nenner überlegt.
Will man Brüche malnehmen, so nimmt man einfach Zähler mit Zähler und Nenner mit Nenner mal. Brüche teilt man, indem man bei dem Bruch, durch den man teilt, Zähler und Nenner vertauscht und dann malnimmt.
Wie nennt man den Zahlbereich, zu dem auch die Brüche (größer oder kleiner Null) gehören?
Das sind die rationalen Zahlen.