Rechtwinkliges Dreieck

Dieses Skript führt Berechnungen an einem rechtwinkligen Dreieck mit Hilfe des Satzes des Pythagoras durch.

Zwei beliebige Felder sind auszufüllen. Rest wird berechnet

Seite a: Seite b: Seite c:
Winkel Alpha:Winkel Beta
p: q: Höhe h:
Flächeninhalt:

Du hast Mathefragen? Schau immer erst bei Mathepower.com!

Für rechtwinklige Dreiecke mit rechtem Winkel bei C gilt:
Flächeninhalt = (a * b) / 2
a² + b² = c² (Satz des Pythagoras)
a² = c * p, b² = c * q (Kathetensatz des Euklid)
h² = p * q (Höhensatz des Euklid)
sin Alpha = a / c

Rechtwinklige Dreiecke

Was ist ein rechtwinkliges Dreieck?

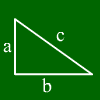
Ein rechtwinkliges Dreieck ist ein Dreieck, das einen rechten Winkel zwischen zwei Seiten enthält, also einen 90-Grad-Winkel. Durch diese Eigenschaft kann man an ihm besonders leicht Berechnungen durchführen. Daher nimmt man in der Schule meist zuerst rechtwinklige Dreiecke durch und versucht dann, aus ihnen Rechenregeln für allgemeine Dreiecke herzuleiten.
Die Seite gegenüber vom rechten Winkel nennt man übrigens Hypotenuse, die beiden anderen Seiten Katheten.
Im Beispieldreieck links ist der rechte Winkel gegenüber von c. Daher ist c eine Hypotenuse und a und b sind Katheten.

Welche Rechenregeln gelten für rechtwinklige Dreiecke?

In rechtwinkligen Dreiecken gilt der Satz des Pythagoras: a²+b²=c². Das heißt also umgekehrt: c=Wurzel aus (a²+b²) oder b=Wurzel aus (c²-a²). Auf diese Weise kann man aus zwei gegebenen Seiten leicht die dritte berechnen.

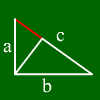
Weiter gilt für die Abschnitte der Hypotenuse, die p und q heißen, wobei p der Abschnitt unter a und q der unter b ist (siehe z.B. p im Bild links):
a²=c*p und b²=c*q (Kathetensatz).
Als drittes gilt noch der Höhensatz, der folgende Aussage über die Höhe auf der Seite c macht: h²=p*q.
Den Flächeninhalt eines rechtwinkligen Dreieckes kann man auch recht einfach berechnen, da er einfach gleich (Kathete*andere Kathete)/2 ist.

Für weitere Infos zu rechtwinkligen Dreiecken bewege die Maus einfach über einen der Begriffe unten, und der entsprechende Teil des Dreiecks wird farbig markiert.
Ein rechtwinkliges Dreieck.

Kathete a, Kathete b, Hypotenuse c,
Hypotenusenabschnitt p, Hypotenusenabschnitt q, Flächeninhalt, Höhe auf c

Satz des Pythagoras

Wie beweist man den Satz des Pythagoras?

Eine Möglichkeit, den Satz zu beweisen, zeigt unsere Flash-Animation:

Berechne bei Mathepower deine Aufgaben zum Satz des Pythagoras. Die Formel lautet a² + b² = c². Mathepower kann Berechnungen am rechtwinkligen Dreieck durchführen. Auch Kathetensatz und Höhensatz des Euklid kann man mit Mathepower berechnen. Flächenberechnung, Seitenberechnung und Winkelberechnung sind auch kein Problem. Ein rechter Winkel ist erforderlich, damit man den Satz des Pythagoras anwenden darf. Gegenkathete, Ankathete und Hypotenuse werden problemlos berechnet.

Gefällts dir hier? Mathepower zu den Favoriten hinzufügen und wiederkommen!